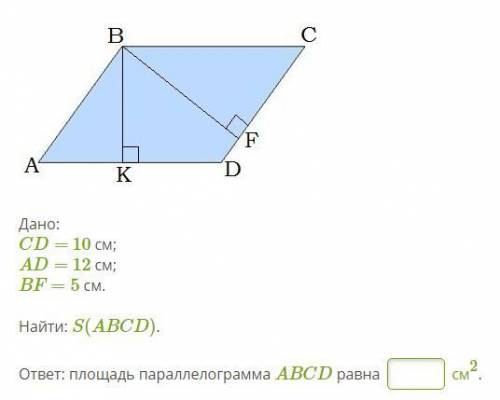
(легко)(геометрия) Дано:
CD= 10 см;
AD= 12 см;
BF=5 см.

Найти: S(ABCD).

ответ: площадь параллелограмма ABCD равна

см2.

площадь параллелограмма равна произведению стороны на высоту проведенную к этой стороне

Объяснение:

s=cd*bf=10*5=50см^2

50

Объяснение:

S(ABCD)=BF*CD=5*10=50

Для того чтобы найти площадь параллелограмма ABCD, нужно знать длину его основания и высоту.

В данной задаче основаниями параллелограмма являются отрезки AD и BC, а высотой является отрезок BF.

Для начала, найдем высоту параллелограмма:

1. Поскольку параллелограмм ABCD является поворотом прямоугольника ABFE науголник от C с противоположным углом B (изображена на рисунке), то высоты обоих фигур совпадают.

2. Заметим, что треугольник BFC является прямоугольным, потому что угол B равен 90 градусов.

3. Используя теорему Пифагора в прямоугольном треугольнике BFC, найдем длину высоты BF:
BF² = BC² - FC²
BF² = BC² - (BF - FC)² (поскольку BF = FC)
BF² = BC² - (5 см - FC)²

4. Так как CD является биссектрисой угла поворота, то отрезок FC делит CD пополам, и FC = 10 см / 2 = 5 см.

5. Подставим FC = 5 см в предыдущее уравнение:
BF² = BC² - (5 см - 5 см)²
BF² = BC² - 0²
BF² = BC²

Из уравнения выше видно, что BF равна BC. Поэтому BF = BC = 5 см.

Теперь, когда у нас есть основание параллелограмма (AD = 12 см) и его высота (BF = BC = 5 см), мы можем найти площадь параллелограмма ABCD:

S(ABCD) = AD * BF
S(ABCD) = 12 см * 5 см
S(ABCD) = 60 см²

Таким образом, площадь параллелограмма ABCD равна 60 см².