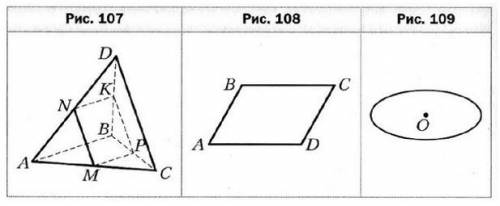
КР-2. Вариант 2. 1. Точки М, N, К и Р — середины рёбер АС, AD, BD и ВС тетраэдра DABC соответственно, АВ = 30 см, CD = 26 см (рис. 107). Докажите, что точки М, N, К и Р являются вершинами параллелограмма, и вычислите периметр этого параллелограмма.
2. Плоскость γ пересекает стороны DE и DF треугольника DEF в точках В и С соответственно и параллельна стороне EF, CD : CF = 3:7, ВС = 9 см. Найдите сторону EF треугольника.
3. Параллелограмм ABCD является изображением квадрата A1B1C1D1 (рис. 108). Постройте изображение радиуса вписанной окружности квадрата, проведённого в точку касания этой окружности со стороной А1D1.
4. Плоскости α и β параллельны. Через точку О, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках А1 и В1, а другая — в точках А2 и В2 соответственно. Найдите отрезок В1В2, если он на 3 см меньше отрезка А1А2, А2В2 = 18 см, ОА2 = 10 см.
5. Эллипс с центром О является изображением окружности с центром O1 (рис. 109). Постройте изображение двух перпендикулярных диаметров этой окружности.

v201612    3   01.12.2020 13:18    419