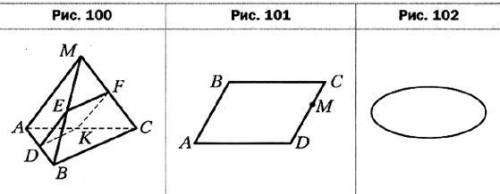
КР-2. Вариант 1. 1. Точки D, Е, F и К — середины рёбер АВ, МВ, МС и АС тетраэдра МАВС соответственно, ВС = 42 см, AM = 36 см (рис. 100). Докажите, что точки D, Е, F и К являются вершинами параллелограмма, и вычислите периметр этого параллелограмма.
2. Плоскость β пересекает стороны АС и ВС треугольника АВС в точках Е и F соответственно и параллельна стороне АВ, АЕ : СЕ = 5:2, АВ = 21 см. Найдите отрезок EF.
3. Параллелограмм ABCD является изображением ромба A1B1C1D1, точка М — изображение некоторой точки M1 отрезка C1D1 (рис. 101). Постройте изображение перпендикуляра, опущенного из точки М1 на диагональ B1D1 ромба.
4. Плоскости β и γ параллельны. Из точки А, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости β и γ в точках В1 и С1, а другой — в точках В2 и С2 соответственно. Найдите отрезок С1С2, если он на 14 см больше отрезка В1В2, АС1 =11 см, В1С1 = 7 см.
5. Дан эллипс, являющийся изображением окружности с центром О (рис. 102). Постройте изображение точки О.

MCKOLYA    2   01.12.2020 13:16    332