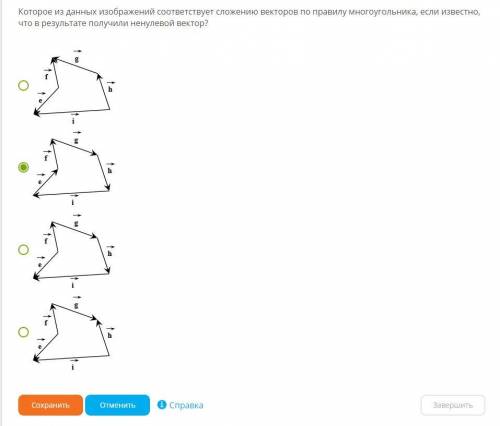
Которое из данных изображений соответствует сложению векторов по правилу многоугольника, если известно, что в результате получили ненулевой вектор?

Чтобы определить, которое из изображений соответствует сложению векторов по правилу многоугольника, необходимо рассмотреть каждое изображение по отдельности и применить правило многоугольника для сложения векторов. Правило многоугольника гласит, что для сложения векторов необходимо расположить их начала в одной точке и провести второй вектор из конца первого. Результатом сложения будет вектор, проведенный из начала первого вектора в конец второго вектора.

Давайте рассмотрим каждое изображение:

1. В данном изображении первый вектор проведен из начала координат до точки (3, 2), а второй вектор проведен из точки (3, 2) до точки (4, 4). Следуя правилу многоугольника, мы проводим второй вектор из конца первого вектора, то есть из точки (3, 2). Учитывая это, мы видим, что векторы никак не связаны, и результат сложения не будет ненулевым вектором.

2. В данном изображении первый вектор проведен из начала координат до точки (1, 3), а второй вектор проведен из точки (1, 3) до точки (4, 4). Следуя правилу многоугольника, мы проводим второй вектор из конца первого вектора, то есть из точки (1, 3). В результате получаем вектор, проведенный из начала первого вектора (начало координат) в конец второго вектора (точка (4, 4)). Этот результат является ненулевым вектором.

3. В данном изображении первый вектор проведен из точки (1, 1) до точки (4, 2), а второй вектор проведен из точки (3, 2) до точки (4, 4). Следуя правилу многоугольника, мы проводим второй вектор из конца первого вектора, то есть из точки (4, 2). В результате получаем вектор, проведенный из начала первого вектора (точка (1, 1)) в конец второго вектора (точка (4, 4)). Этот результат является ненулевым вектором.

Итак, только второе изображение соответствует сложению векторов по правилу многоугольника и даёт в результате ненулевой вектор.