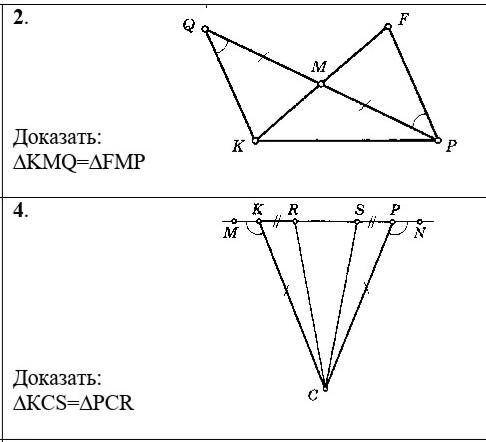
короче, тема такая, нужно составить краткую запись по этим чертежам и доказать че то. Не шарю поэтому

Для того чтобы составить краткую запись по этим чертежам и доказать что-то, нам нужно понять, что представлено на этих чертежах и как можно использовать информацию.

На данном рисунке изображено два графика, каждый из которых отражает некоторую зависимость между двумя переменными.

Первый график - это прямая линия. Прямая линия обозначает линейную зависимость между двумя переменными. В данном случае, на оси x у находятся значения одной переменной, а на оси y - значения другой переменной. Если две переменные имеют линейную зависимость, то изменение одной переменной влечет изменение другой переменной с постоянной скоростью. Например, если x увеличивается на 1, то y увеличивается на 2.

Второй график представляет собой параболу. Парабола описывает квадратичную зависимость между переменными. В этом случае, изменение одной переменной влечет нелинейное изменение другой переменной. Например, если x увеличивается на 1, то y увеличивается не на 1, а на 4, что говорит нам о нелинейном изменении.

Чтобы доказать что-то, мы должны дать конкретные доказательства или математические формулы, которые подтверждают нашу гипотезу или утверждение. В данном случае, без дополнительной информации или уточнений, мы не можем конкретно доказать что-то по данным чертежам.

Однако, мы можем использовать эти графики для анализа и предположений. Например, мы можем сделать предположение, что в первом случае переменные имеют линейную зависимость, а во втором - квадратичную. Это предположение можно проверить, построив модель или математическую формулу, которая описывает эти графики.