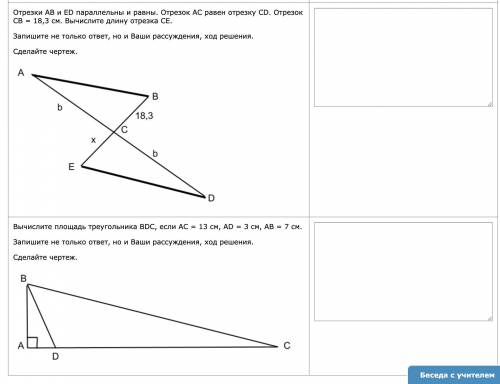
КИНУ 100 РУБ КТО СДЕЛАЕТ ПРОСТУЮ ГЕОМЕТРИЮ 7 КЛАСС Длина основания равнобедренного треугольника на 26 см меньше его боковой стороны. Периметр треугольника 124 см. Найдите стороны треугольника. Запишите не только ответ, но и Ваши рассуждения, ход решения. Даны два смежных угла. Биссектриса первого из них образует угол 32 градуса с общей стороной этих углов. Найдите величину обоих смежных углов. Запишите не только ответ, но и Ваши рассуждения, ход решения. В треугольнике АВС средние линии образуют треугольник PNM. PN=22 см, PM=19 см, NM= 5 см. Найдите периметр треугольника АВС. Отрезки АВ и ED параллельны и равны. Отрезок АС равен отрезку СD. Отрезок СВ = 18,3 см. Вычислите длину отрезка СЕ. Запишите не только ответ, но и Ваши рассуждения, ход решения. Вычислите площадь треугольника BDC, если АС = 13 см, AD = 3 см, АВ = 7 см. Запишите не только ответ, но и Ваши рассуждения, ход решения. ЧЕКАЙТЕ СКРИНЫ

Давайте начнем с первого вопроса. Вам нужно найти стороны равнобедренного треугольника.

Пусть сторона треугольника равна "х". Тогда основание будет иметь длину "х - 26".

Периметр треугольника составляет 124 см, поэтому мы можем написать уравнение:

х + х + (х - 26) = 124

Решим это уравнение:

3х - 26 = 124

3х = 150

х = 50

Итак, сторона треугольника равна 50 см, а основание равно 24 см (50 - 26).

Перейдем к следующему вопросу. У нас есть два смежных угла с биссектрисой. Давайте назовем эти углы "А" и "В". Пусть угол "В" будет больше угла "А".

Угол "В" разделен на две части биссектрисой, обозначим одну из этих частей как "С". Угол "С" равен 32 градусам. Также у нас есть угол "А".

Сумма углов треугольника равна 180 градусов, поэтому мы можем написать уравнение:

А + С + С = 180

Разделим 180 на 2, чтобы найти значение одной части суммы углов:

А + 32 = 90

А = 58

Угол "А" равен 58 градусам.

Угол "В" равен 180 - 58 = 122 градусам.

Продолжим с третьим вопросом. У нас есть треугольник АВС, где средние линии образуют треугольник РНМ. Длины средних линий равны: PN = 22 см, PM = 19 см, NM = 5 см.

К сожалению, на переданных изображениях не указано, каким из сторон треугольника АВС соответствуют эти средние линии. Если мы предположим, что Р соответствует стороне АВ, то эта сторона будет равна 2PN = 44 см.

Если другие стороны треугольника АВС также равны 44 см, то периметр треугольника АВС равен 44 + 44 + 44 = 132 см.

Переходим к следующему вопросу. У нас есть параллельные отрезки АВ и ED. Отрезок АС равен отрезку СD. Отрезок СВ равен 18,3 см.

Если отрезок СВ равен 18,3 см, и АС равно СD, то общая длина АС и СD равна 2*18,3 = 36,6 см.

Так как отрезок АС равен СD, то отрезок СЕ равен 36,6/2 = 18,3 см.

Продолжим с последним вопросом. У нас есть треугольник BDC, где АС = 13 см, AD = 3 см и АВ = 7 см.

Чтобы вычислить площадь треугольника BDC, мы можем воспользоваться формулой площади треугольника.

Пусть BD будет основанием треугольника BDC. Тогда его площадь равна:

Площадь = (BD*DC)/2

Мы можем выразить DC через известные стороны треугольника BDC:

DC = AC - AD = 13 - 3 = 10 см

Теперь мы можем вычислить площадь треугольника BDC:

Площадь = (7 * 10)/2 = 35 см²

Таким образом, площадь треугольника BDC равна 35 см².