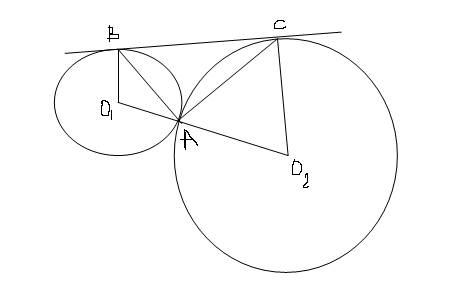
Кдвум окружностям с центрами в точках о1,о2,касающимся внешним образом в точке а, проведена общая касательная вс(в и с-точки ксания).докажите,что угол вас-прямой. я гиа 2015 готовлюсь летом! )
Ответы
Треугольник АСО2 и АВО1 равнобедренные, т.к. стороны - радиусы. Значит углы АСО2=САО2, АВО1=ВАО1. Т.к. уголы В и С = 90 касательная к окружности, то из трапеции ВСО1О2 сумма углов О1 и О2 = 180. Из треугольников АСО2 и АВО1: угол АО1В=180-О1ВА*2, АО2С = 180-2*О2СА. их сумма = 180, значит 180=180-О1ВА*2+180-2*О2СА, т.е. О1ВА+О2СА=90. угол ВСА = 90-О2СА, АВС = 90-О1ВА. Т.к. сумма углов треугольника 180 имеем искомый угол = 180-(90-О2СА)-(90-О1ВА) =О1ВА+О2СА, что как уже ранее рассмотрено =90 .
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Задание: 1. Чья сюита Фрески Дианисия звучала в начале? 2. Из каких инструментов...
2 - Каких приметы времени изобразили Солженицын и Шаламов в своих произведениях?...
2 - написать сочинение о Луизе Кларк из романа До встречи с тобой ...
2 - К режущим инструментам относятся: струбцины рубанок лобзик рейсмус стамеска...
3 - даю 20б, алгебра 2 задания! надеюсь правильно помджете)...
2 - Герои ВОВ которые родились на Витебщине...
1 - Применение роботов в современном мире. Слово «робот» придумано чешским писателем...
2 - 1 запишите в общем виде условный оператор 2 определите тип чисел:15,61.0,2413...
1 - алгебра! Реши систему уравнений методом алгебраического сложения....
1 - 1. При обжиге 200 г известняка выделилось 18 л углекислого газа, составляющего...
1