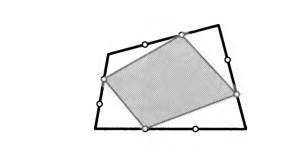
Каждую сторону выпуклого четырехугольника разделили на три равные части. Соответствующие точки соединили так, как
это показано на рисунке. Какую часть исходного четырехугольни­
ка составляет закрашенная фигура?​

Чтобы решить эту задачу, нам нужно определить площадь закрашенной фигуры относительно исходного четырехугольника.

Шаг 1: Разбиение сторон на равные части
Исходя из условия, каждую сторону четырехугольника мы делим на три равные части. В результате получаем точки разбиения. Нарисуем эти точки на рисунке для большей наглядности.

Шаг 2: Соединение точек
Соединим соответствующие точки, чтобы получить закрашенную фигуру. Изобразим это на рисунке.

Шаг 3: Определение площадей
Теперь нам нужно определить площадь исходного четырехугольника и закрашенной фигуры.

Обратимся к геометрии для решения этой задачи. Зная, что площадь многоугольника можно найти, разделив его на прямоугольники, которые мы уже знаем площадь.

Исходный четырехугольник можно разделить на шесть прямоугольников, из которых два крайних имеют общую сторону с исходным четырехугольником, а четыре прямоугольника разделены на два треугольника. Высоты треугольников равны двум третям стороны соответствующего прямоугольника.

Пусть длина сторона исходного четырехугольника равна L. Тогда длина каждого из шести прямоугольников будет равна L/3 (так как сторону разделили на три равные части).

Рассмотрим крайние прямоугольники. Они будут иметь площадь L * (L/3) = (L^2)/3.

Рассмотрим четыре прямоугольника, разделенные на два треугольника. Площадь каждого прямоугольника будет равна L/3 * (L/3) = (L^2)/9.

Высоты треугольников составляют 2L/3, поэтому площадь каждого треугольника будет (1/2) * (2L/3) * (L/3) = (L^2)/9.

Теперь посчитаем площадь всего исходного четырехугольника.

Общая площадь исходного четырехугольника = 2 * (L^2)/3 + 4 * (L^2)/9
Общая площадь исходного четырехугольника = (4L^2 + 8L^2)/9
Общая площадь исходного четырехугольника = (12L^2)/9
Общая площадь исходного четырехугольника = (4L^2)/3

Теперь посчитаем площадь закрашенной фигуры.

Закрашенная площадь = площадь исходного четырехугольника - площадь четырех треугольников
Закрашенная площадь = (4L^2)/3 - 4 * (L^2)/9
Закрашенная площадь = (12L^2 - 4L^2)/9
Закрашенная площадь = (8L^2)/9

Таким образом, закрашенная фигура составляет (8L^2)/9 часть исходного четырехугольника. Ответом на задачу будет (8L^2)/9.