Катет BC прямоугольного треугольника ABC равен 10 . Через вершину прямого угла C проведена прямая, от которой вершина A удалена на 3 , а вершина B — на 8 . Определите квадрат гипотенузы AB .
Другие вопросы по теме Геометрия
Популярные вопросы
- Умоляю добрые все ! )если вы решите : трапеция abcd аd параллельна bc и пересекают...
1 - Озаглавьте текст. укажите предложения, которые связаны с местоимений. спишите,...
1 - Назовите горячие точки холодной войны...
3 - Как сделать? прописи 1 класс ,1 часть...
3 - К57 г 5% раствора соли добавили 43 г воды. найдите массовую долю соли в новом растворе....
3 - 2. сравним два мнения. кто из участников спора прав? любитель вина: «употребление...
1 - На заряженную частицу влетающую в однородное магнитное поле с индукцией 0,25 тл,...
2 - Сетактический разбор предложения.максим сильно нажал на кнопку дверного звонка...
1 - Как изобразительно-выразительные средства писателю создать картины природы? нужно...
2 - Вопрос по пат анатомии, какой это компенсаторный процесс?...
3
(см. объяснение)
Объяснение:
Первый
Пусть ∠ECB=a. Тогда, т.к. ∠ACB=90°, то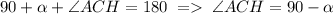 . Соответственно
. Соответственно  . Значит треугольник AHC подобен треугольнику BEC по двум углам (∠AHC=∠BEC=90° и ∠ECB=∠HAC=
. Значит треугольник AHC подобен треугольнику BEC по двум углам (∠AHC=∠BEC=90° и ∠ECB=∠HAC=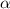 ). Из подобия следует, что
). Из подобия следует, что 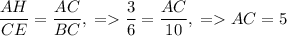 . Тогда по теореме Пифагора для ΔABC:
. Тогда по теореме Пифагора для ΔABC: 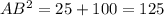 .
.
Приведу решение, в котором используется только теорема Пифагора:
Пусть AC=x. AH=3, а BE=8. Тогда из прямоугольного треугольника AHC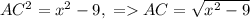 . Из прямоугольного треугольника BCE
. Из прямоугольного треугольника BCE 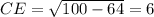 . Значит
. Значит 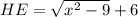 . Проведем AF - высоту из точки A на BE. Тогда AFEH - прямоугольник =>
. Проведем AF - высоту из точки A на BE. Тогда AFEH - прямоугольник => 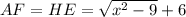 . По теореме Пифагора для прямоугольного треугольника AFB
. По теореме Пифагора для прямоугольного треугольника AFB 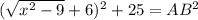 . Но с другой стороны из прямоугольного треугольника ABC
. Но с другой стороны из прямоугольного треугольника ABC 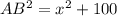 , т.е. получили уравнение
, т.е. получили уравнение 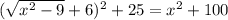 , откуда x=5, а значит
, откуда x=5, а значит 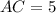 . Тогда
. Тогда 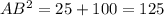 .
.
Задача решена!