Каковы координаты вектора, который разложен на координатные векторы i→ и j→ следующим образом:
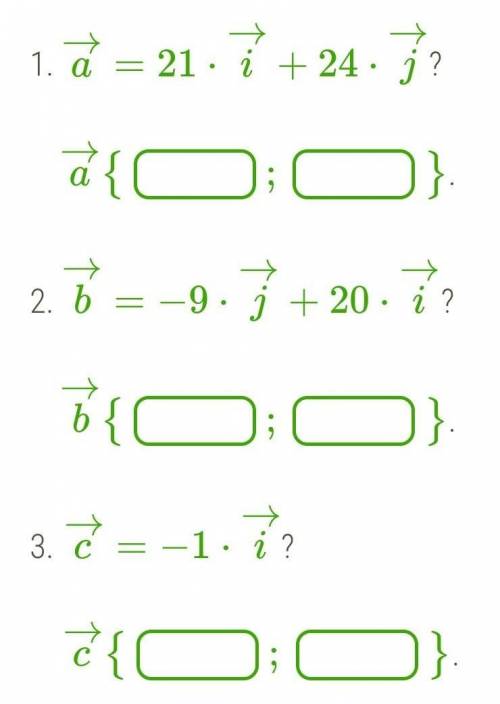
Другие вопросы по теме Геометрия
Популярные вопросы
- Какие программы относятся к программам обработки мультимедийных...
3 - Придумайте число , которое оканчивается на 11, делится на 11 и...
2 - Сколько полных оборотов сделала земля с 15.01.2008...
1 - Sos прочитай рассказ мэг и поставь если верно,а если нет то минус....
1 - От станции а до станции в поезд идет 7,8 часов.если скорость поезда...
1 - Выразите в часах 4 минуты 17 минут 54 секунды...
2 - Прямые и плоскости в пространстве верно ли утверждение: наклонная...
2 - Танк и самолёт стоят 29 рублей, танк и динозавр – 24 рубля, самолёт...
2 - Около правильной шестиугольной призмы описана сфера радиуса 5 см....
2 - Придумай 3 вопроса по произведению и.с.никитина русь...
2
Для определения проекций воспользуемся формулами проекций:
Px = |P| * cos(θ) , Py = |P| * sin(θ),
где Px и Py - проекции вектора Р на оси x и y соответственно, |P| - длина вектора Р, θ - угол между вектором Р и положительным направлением оси x.
Обратите внимание, что угол θ в данной задаче равен 30°, так как вектор Р разложен на координатные векторы i и j под углом 30°.
Таким образом, получаем:
Px = |P| * cos(30°) = |P| * √3/2,
Py = |P| * sin(30°) = |P| * 1/2.
Теперь нам осталось найти длину вектора Р. Для этого воспользуемся формулой длины вектора:
|P| = √(Px² + Py²).
Подставляем значения проекций в эту формулу:
|P| = √((|P| * √3/2)² + (|P| * 1/2)²).
Воспользуемся свойством равенства для квадрата суммы двух чисел:
|P| = √((|P|² * 3/4) + (|P|² * 1/4)),
|P| = √(|P|² * (3/4 + 1/4)),
|P| = √(|P|² * 1) = √(|P|²) = |P|.
Таким образом, получаем, что длина вектора Р равна |P|.
Итак, координаты вектора Р: (Px, Py) = (|P| * √3/2, |P| * 1/2).