1. Геометрия
  2. Kаковы должны быть размеры закрытого

Kаковы должны быть размеры закрытого цилиндрического бака объёмом 170,368π, чтобы на его изготовление ушло наименьшее количество материала?

7432999 7432999    3   02.03.2021 23:58    7

Ответы
Sharapov2000 Sharapov2000  02.04.2021 00:06

Объём цилиндра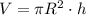 V = \pi R^2\cdot h

Площадь полной поверхности цилиндра

S = 2\pi R^2 + 2\pi R\cdot h

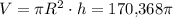
Итак V = \pi R^2 \cdot h = 170{,}368\pi

R^2 \cdot h = 170{,}368

h = \frac{170{,}368}{R^2}

S = 2\pi R^2 + 2\pi R\cdot\frac{170{,}368}{R^2} =

= 2\pi R^2 + 2\pi\cdot\frac{170{,}368}{R}

Найдём экстремум функции

S = 2\pi R^2 + 2\pi\cdot\frac{170{,}368}{R}

S' = 4\pi R - 2\pi\cdot\frac{170{,}368}{R^2} =

= 4\pi\cdot\frac{ R^3 - 85{,}184 }{R^2} =

= 4\pi\cdot\frac{ (R - 4{,}4)\cdot ( R^2 + 4{,}4\cdot R + (4{,}4)^2 )}{R^2}

Очевидно, что R > 0.

Тогда минимум в точке R = 4,4. Тогда

h = \frac{170{,}368}{(4{,}4)^2} = \frac{170{,}368}{19{,}36} = 8{,}8

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Боженька206 Боженька206  17.07.2019 22:40
Кто и в каком городе придумал радиосвязь...
LuLu6780 LuLu6780  17.07.2019 22:40
Два угла одного треугольника 1240 и 360 , а два угла другого треугольника 200 и 360 . подобны ли треугольники?...
ziminasofa2703 ziminasofa2703  23.04.2020 12:42
2. если ты посмотришь видеоматериал, то тебе будет легче освоить этот материал 3. открой файл №1 и реши задачу под №...
dmolodozhnikovp02gx5 dmolodozhnikovp02gx5  23.04.2020 12:42
Дан треугольник ABC, в котором AC=4, BC=7, AB=6. Найдите Сos Дайте развернутый ответ...
vhovalyg90 vhovalyg90  23.04.2020 12:42
Решите!!CG — биссектриса угла DCE.Вычисли угол DCG, если ∢DCE=74°.∢DCG=...
Аделя6661 Аделя6661  23.04.2020 12:42
Расставит знаки применения.тропинка обогнула куст орешника лес сразу раздался в стороны посреди поляны стоял огромный и величественный дуб деревья почтительно расступились перед ним...
mandarinka3001 mandarinka3001  23.04.2020 12:42
а то я полный 0 в геометрии....
Камила070 Камила070  23.04.2020 12:41
решить задачу по геометрии, очень Из точки К биссектриса острого угла C проведены перпендикуляры AB и CB к сторонам этого угла. Докажите что АВ перпендикулярна КС...
pamagiteplease pamagiteplease  23.04.2020 12:41
Как скинуть фото с/р чтобы вам было понятно...
алиса2343 алиса2343  05.06.2020 08:13
усеченная пирамида. Нужно найти высоту и апофему. картинка конечно не очень, угол С там не видно, но надеюсь чета хоть поймёте...

Популярные вопросы