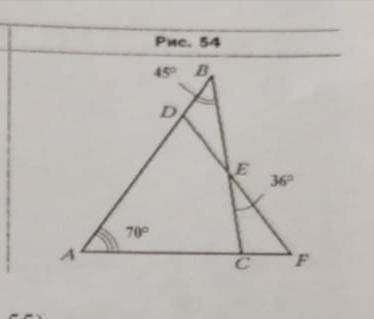
Какова градусная мера угла F, изображённого на рисунке 54?

45 градусов.

Объяснение:

т.к. углы соотвентственные

На рисунке 54 нам дан треугольник ABC, а нам нужно найти градусную меру угла F. Для решения этой задачи нам понадобятся два утверждения о сумме углов треугольника:
1. Сумма всех углов в треугольнике равна 180 градусам.
2. Угол, напротив наибольшей стороны, является наибольшим углом треугольника.

Давайте решим эту задачу пошагово:

Шаг 1: Сначала найдем длины сторон треугольника ABC. По рисунку мы видим, что сторона AC равна 11 см, сторона BC равна 6 см, а сторона AB равна 10 см.

Шаг 2: Теперь найдем наибольшую сторону треугольника. Мы видим, что сторона AC равна 11 см, и это наибольшая сторона.

Шаг 3: Используя второе утверждение о сумме углов треугольника, мы можем заключить, что угол F является наибольшим углом треугольника ABC.

Шаг 4: Теперь найдем градусную меру угла F. Для этого воспользуемся теоремой косинусов, которая гласит:

c^2 = a^2 + b^2 - 2ab * cos(C),

где a, b, и c - стороны треугольника, а C - противолежащий угол.

В нашем случае a = 6, b = 10 и c = 11.

Подставим эти значения в формулу:

11^2 = 6^2 + 10^2 - 2 * 6 * 10 * cos(F).

121 = 36 + 100 - 120 * cos(F).

121 = 136 - 120 * cos(F).

-15 = -120 * cos(F).

Теперь разделим обе части уравнения на -120:

-15 / -120 = cos(F).

1 / 8 = cos(F).

Поскольку мы знаем, что cos(F) равно 1/8, мы можем использовать обратную функцию cos^(-1) для нахождения градусной меры угла F. Воспользуемся калькулятором и найдем:

F ≈ 82.81 градусов.

Таким образом, градусная мера угла F, изображенного на рисунке 54, примерно равна 82.81 градусам.