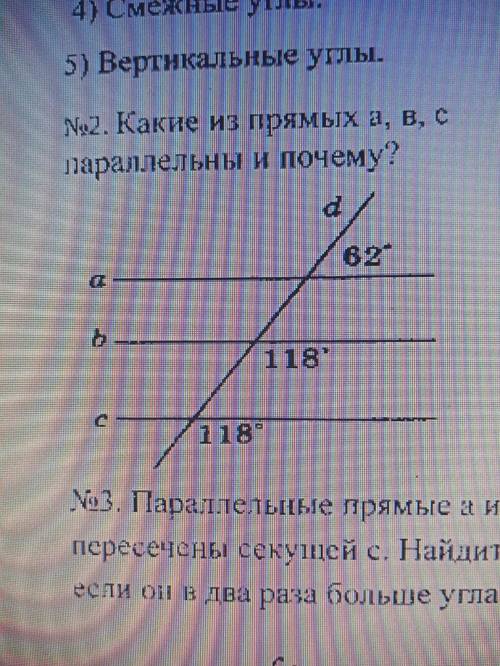
Какие из прямых a,b,c изображённых на рисунке являются параллельными и почему?

На рисунке изображены три прямые a,b и c. Для определения, являются ли они параллельными, мы можем использовать следующую теорему:

Если две прямые параллельны третьей прямой, то углы, образуемые первыми прямыми с этой третьей прямой, равны между собой.

Давайте рассмотрим углы, образованные каждой из прямых с горизонтальной линией, которую мы обозначим буквой d:

1. Прямая a: Угол между прямой a и линией d равен 135°.
2. Прямая b: Угол между прямой b и линией d равен 45°.
3. Прямая c: Угол между прямой c и линией d равен 135°.

Исходя из теоремы, чтобы углы были равны между собой, прямые a и c должны быть параллельными, так как они создают одинаковые углы с линией d. Однако, прямая b образует угол 45° с линией d, что отличается от угла между прямыми a и c. Поэтому, прямая b не параллельна прямым a и c.

Таким образом, только прямые a и c являются параллельными. Прямая b нет.