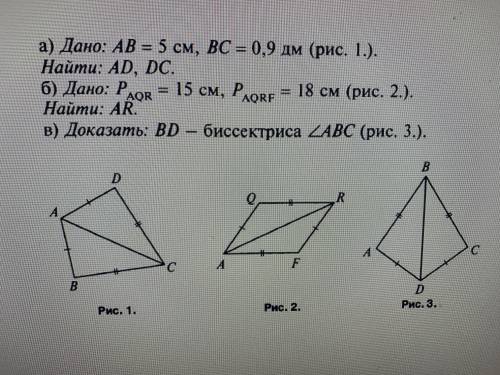
Как доказать по 3 признаку задачи номер 2 и номер 3?
заранее.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.ситаксический разбор слов. 2.морфорный разбор слов. кошка царапнула...
3 - Укажите категории землевладельцев xvii в. 1ремесленники 2церковь 3бояре...
1 - Грузовик размеры которого 6м*3м*7,5м надо установить коробки с консервами...
3 - Первый множитель неизвестен а второй равен 10...
2 - Система: a+x= 4 3a+4x =x^2 3a=x найти все значения а при которых система...
3 - Вклетчатом квадрате саша отметила клетку.оказалось что в своем столбце...
3 - Запиши произведение в котором первый множитель равен 9 а второй неизвестен...
1 - 30 ! какой объем (н. у.) аммиака можно получить, если известно, что в...
3 - Все матереки на планете и сколько их...
1 - Лежат ли точки a(3; 7: 4),b(2: -1: -1),c(4; 15; 9) на одной прямой ?...
2
Для начала, давайте вспомним, что представляет собой 3 признак задачи в аналитической геометрии. Этот признак определяет, что если три точки находятся на одной прямой, то их координаты будут удовлетворять линейному уравнению вида ax + by = c.
Прежде чем приступить к доказательству, давайте рассмотрим каждую задачу по отдельности.
Zадача номер 2:
На рисунке даны точки А(1, 2), В(3, 6) и С(5, 10), и нам нужно проверить, лежат ли они на одной прямой.
1. Выразим коэффициенты a, b и c, подставив координаты точек в уравнение ax + by = c:
Для точки A(1, 2):
x = 1, y = 2: a * 1 + b * 2 = c
Для точки B(3, 6):
x = 3, y = 6: a * 3 + b * 6 = c
Для точки C(5, 10):
x = 5, y = 10: a * 5 + b * 10 = c
2. Теперь составим систему уравнений и решим ее для a, b и c:
{ a + 2b = c
{ 3a + 6b = c
{ 5a + 10b = c
После решения этой системы уравнений, мы должны получить одинаковые значения для a, b и c, чтобы убедиться, что точки А, В и С лежат на одной прямой.
Zадача номер 3:
На рисунке даны точки D(1, 2), Е(3, 4) и F(4, 6), и нам также нужно проверить, лежат ли они на одной прямой.
1. Выразим коэффициенты a, b и c, подставив координаты точек в уравнение ax + by = c:
Для точки D(1, 2):
x = 1, y = 2: a * 1 + b * 2 = c
Для точки E(3, 4):
x = 3, y = 4: a * 3 + b * 4 = c
Для точки F(4, 6):
x = 4, y = 6: a * 4 + b * 6 = c
2. Как и в задаче номер 2, составим систему уравнений и решим ее для a, b и c:
{ a + 2b = c
{ 3a + 4b = c
{ 4a + 6b = c
После решения этой системы уравнений, мы должны получить одинаковые значения для a, b и c, чтобы убедиться, что точки D, E и F лежат на одной прямой.
Это подробное решение должно быть понятным школьнику. Давайте теперь решим эти задачи и проверим, лежат ли точки на одной прямой.