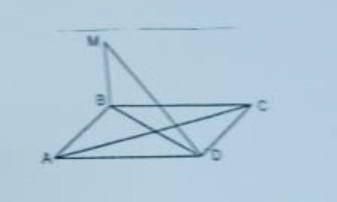
: К плоскости ромба ABCD проведён перпендикуляр BM, равный 11✓3 см. AB = 11см, угол А = 60°. Найти угол между MD и плоскость ромба.

Для решения данной задачи мы можем использовать свойства ромба и понятие перпендикуляра.

Нам дано, что BM - перпендикуляр к плоскости ромба ABCD и его длина равна 11√3 см. Также, известно, что AB = 11 см и угол А равен 60°.

Из свойств ромба мы знаем, что его диагонали пересекаются под прямым углом. Поэтому MD является диагональю ромба.

Мы знаем, что AB = CD = 11 см, так как это свойство ромба.

Также, у нас есть прямоугольный треугольник BMη, где BM = 11√3 см, η = 60° (так как угол А = 60°) и BN - высота перпендикуляра, проведенного из вершины B на сторону CD.

Мы можем найти BN, используя тригонометрическую функцию синуса:

sin(η) = BN / BM

sin(60°) = BN / 11√3

√3/2 = BN / 11√3

2 * √3 * 11√3 = BN

2 * 11 = BN

BN = 22 см

Таким образом, мы нашли, что BN = 22 см.

Теперь мы можем использовать теорему Пифагора для нахождения MD:

MD^2 = AB^2 + BN^2

MD^2 = 11^2 + 22^2

MD^2 = 121 + 484

MD^2 = 605

MD = √605 см

Таким образом, мы нашли, что длина диагонали MD равна √605 см.

Нам нужно найти угол между MD и плоскостью ромба. Можно заметить, что диагональ MD и диагональ CA противоположным сторонам ромба и должны образовывать прямой угол. Это означает, что угол между MD и плоскостью ромба равен 90°.