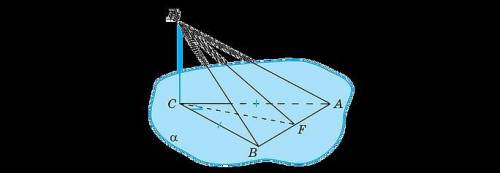
К плоскости равнобедренного прямоугольного треугольника ABC с гипотенузой AB=12√3 см проведён перпендикуляр DC, равный 18 см. Найди угол между плоскостями DAB и CAB. Решение.
Треугольники ABC и ADB равнобедренные: △ABC , а в △ADB DA= , так как эти стороны — . Поэтому медианы CF и DF этих треугольников, проведённые из вершин C и D к общему основанию , являются , и, следовательно, ∠DFC — линейный угол , а значит, угол между плоскостями DAB и CAB равен ∠ . △DFC прямоугольный, DC= , CF= 1/2 = см и поэтому tg∠DFC= = = , откуда ∠DFC= . Заполните пропуски

Для нахождения угла между плоскостями DAB и CAB, мы можем использовать свойство равнобедренных треугольников и определить отношение между стороной треугольника DFC и углом DFC.

Итак, давайте рассмотрим плоскость равнобедренного прямоугольного треугольника ABC. У нас есть гипотенуза AB, которая равна 12√3 см.

Теперь построим перпендикуляр DC к плоскости ABC, который имеет длину 18 см.

Мы видим, что треугольники ABC и ADB являются равнобедренными, так как сторона AB является гипотенузой и стороны DA и DB являются равными (DA=BD).

Медианы CF и DF этих треугольников, проведенные из вершин C и D к общему основанию AB, являются пересекающимися, и поэтому угол DFC является линейным углом между DF и CF.

Для нахождения значения этого угла, мы можем рассмотреть прямоугольный треугольник DFC.

Известно, что DC=18 см и CF=1/2AB. Поэтому CF=1/2 * 12√3 = 6√3 см.

Теперь мы можем использовать тангенс угла DFC, чтобы найти его значение. Тангенс угла может быть найден как отношение противоположной стороны (DF) к прилежащей стороне (CF).

tg∠DFC = DF/CF

Мы знаем, что DF=DC=18 см и CF=6√3 см.

tg∠DFC = 18 / 6√3

Для простоты расчета, мы можем сократить длину сторон треугольника на 6 см.

tg∠DFC = (18/6) / √3 = 3/√3

Теперь мы можем рационализировать это выражение, умножив и числитель и знаменатель на √3.

tg∠DFC = (3/√3) * (√3/√3) = 3√3/3 = √3

Таким образом, мы получаем, что tg∠DFC = √3.

Теперь нам нужно найти сам угол ∠DFC. Мы можем использовать тангенсный отношение для нахождения угла.

tg∠DFC = √3

Находим обратный тангенс:

∠DFC = arctg(√3)

Получаем значения угла ∠DFC.