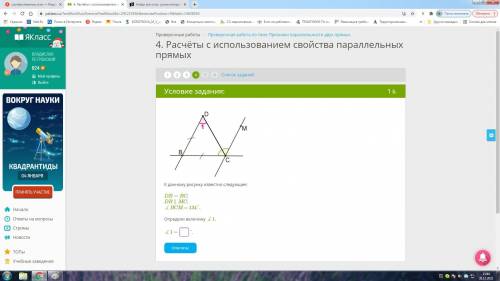
К данному рисунку известно следующее: DB=BC;
DB∥MC;
∡BCM = 134°.

Определи величину ∡1.

67 градусов

Объяснение:

Судя по рисунку, BCD=DCМ=0.5ВСМ=67°

BCD - равнобедренный треугольник, углы при его основании равны, тогда BDC=BCD=67°

Или другим путем с тем же ответом, угол С, смежный углу ВСМ равен 180-134=46°, соответствующий ему DBC при параллельных прямых тоже равен 46°, а углы при основании в треугольнике тогда равны (180-46)/2=67°

ответ: 67°

Объяснение:

посмотрим на угол В с двух сторон

1) т.к. DB+BC, то по свойству углов при основании равнобедренного треугольника ∠1=∠BCD, тогда ∠В=180°-2*∠1,

2) т.к. DB║MC при секущей  ВC, то ∠DBC+∠ВСM=180°как сумма внутренних односторонних, тогда ∠В=180°-∠ВСM=180°-134°=46°

сопоставляем 1) и 2), получаем, 180°-2*∠1=46°⇒∠1=(180°-46°)/2=134°/2=67°

-короче, т.к. ∠1=∠DCB, и ∠1=DСМ, как внутренние накрест лежащие при DB║MC и секущей  DC, то ∠1=∠DCB=∠DСМ=134°/2=67°