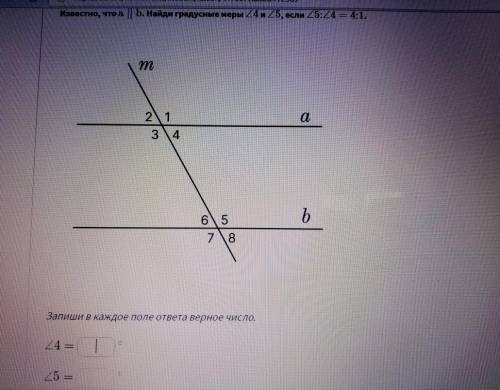
Известно, что a || b. Найди градусные меры угла 4 и угла 5, если угол5:угол4 = 4:1.

Чтобы решить эту задачу, нам понадобятся свойства параллельных линий и соотношение углов.

По условию, мы знаем, что линии a и b параллельны. В параллельных линиях, у соответствующих углов (которые находятся по одну сторону от пересекаемой прямой), равны. То есть угол 4 и угол 5 являются соответствующими углами и, следовательно, их градусные меры тоже равны.

Соотношение углов дано в виде "угол 5 : угол 4 = 4 : 1". Это означает, что градусная мера угла 5 в 4 раза больше градусной меры угла 4.

Давайте обозначим градусную меру угла 4 как x. Тогда градусная мера угла 5 будет 4x.

Таким образом, у нас есть система уравнений:
угол 4 = x
угол 5 = 4x

Теперь нам нужно найти значения x и 4x. Для этого нам понадобится информация о сумме углов в треугольнике, так как углы 4 и 5 образуют треугольник.

Сумма градусных мер углов в треугольнике равна 180 градусов. Поэтому мы можем записать уравнение:
угол 4 + угол 5 + угол 6 = 180

Мы знаем, что угол 6 равен 180 градусов, так как линии a и b параллельны.

Теперь мы можем подставить наши значения углов:
x + 4x + 180 = 180

Мы можем сократить одну 180 на обеих сторонах уравнения:
5x = 0

Таким образом, значение x равно 0.

Теперь у нас есть значение угла 4: x = 0. Мы можем подставить его обратно в уравнение для угла 5 и найти его значение:
угол 5 = 4x = 4 * 0 = 0

Таким образом, градусная мера угла 4 равна 0 градусов, а градусная мера угла 5 также равна 0 градусов.

Обратите внимание, что в этой задаче получился особый случай, когда оба угла равны 0 градусов. Это связано с тем, что угол 4 и угол 5 являются вертикальными углами, а параллельные линии a и b в данном случае являются одной и той же прямой. В общем случае, градусные меры углов 4 и 5 будут отличаться от 0 и определяться соответствующими значениями x и 4x.