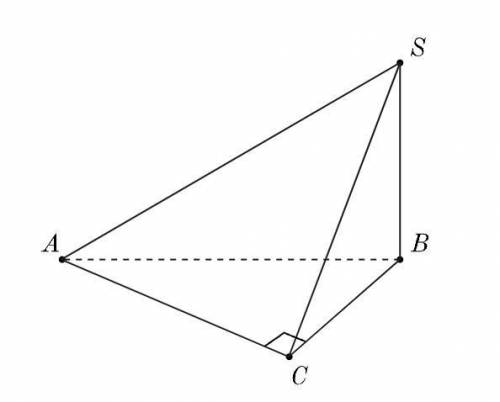
Из точки SS опущен перпендикуляр SBSB к плоскости прямоугольного треугольника ABCABC . Наклонные SASA и SCSC образуют с плоскостью (ABC)(ABC) углы 30{\degree}30° и 45{\degree}45° соответственно. Найди тангенс угла между прямой SASA и плоскостью (SBC)(SBC) , если SB=5SB=5 .
Другие вопросы по теме Геометрия
Популярные вопросы
- Найдите х: 1/(m+n)+(m+n)/x=1/(m-n)+(m-n)/x * 1) (m+n)² 2) другой...
2 - Решите задание на фото даю 12 ладов за ответ...
1 - Растительный и животный мир мëртвого моря и прибрежной части....
1 - Для записи текста используется 256-символьный алфавит. Каждая...
2 - В равнобедренном треугольнике Боковая сторона в два раза больше...
2 - Спишите распределив глаголы в два столбика. Начальная форма...
1 - Характеристика головних героїв вірша В. Сосюри Осінь...
3 - 10) Найдите в метрах длину стороны квадрата D C B Площадь которого...
3 - Что вы узнали о реформах Дарий I ?...
2 - Матроскин продал 42 л молока по 64 руб. за 1 л и 16 кг творога...
2
Для начала, давайте обратимся к информации, данной в условии задачи.
У нас есть прямоугольный треугольник ABCABC, в котором точка SS опущена на сторону AA. Перпендикуляр SBSB опущен из точки SS к плоскости треугольника.
Также, нам известно, что наклонные SASA и SCSC образуют углы 30{\degree}30° и 45{\degree}45° соответственно с плоскостью треугольника.
Наша задача - найти тангенс угла между прямой SASA и плоскостью SBCSBC при условии, что SB=5SB=5.
Чтобы найти тангенс данного угла, нам нужно знать отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике.
Перед тем, как приступить к решению самой задачи, давайте установим некоторые обозначения:
Пусть точка HH - это точка пересечения прямой SASA с плоскостью SBCSBC.
Пусть угол между прямой SASA и плоскостью SBCSBC равен θθ.
Теперь, давайте рассмотрим прямоугольный треугольник SBH:
- Гипотенуза треугольника SBH - это отрезок SB, который равен 5.
- Прилежащий катет - это отрезок HB.
- Противолежащий катет - это отрезок SH.
Так как SBH - прямоугольный треугольник, мы можем использовать соотношение тангенса угла θθ, чтобы найти SH.
Тангенс угла θθ = противолежащий катет (SH) / прилежащий катет (HB).
Мы знаем, что тангенс угла θθ равен 1, так как нити наклонной SASA образует угол 45{\degree}45° с плоскостью SBCSBC (так как угол между наклонной и плоскостью равен 45{\degree}45°).
Таким образом, у нас получается уравнение:
1 = SH / HB
Теперь, нам нужно найти соотношение между противолежащим катетом (SH) и прилежащим катетом (HB).
Мы знаем, что наклонная SASA образует угол 30{\degree}30° с плоскостью треугольника ABCABC.
Из этого угла, мы можем найти sine и cosine этого угла.
sine 30{\degree}30° = противолежащий катет (SH) / гипотенуза треугольника SBH (SB).
cosine 30{\degree}30° = прилежащий катет (HB) / гипотенуза треугольника SBH (SB).
Мы знаем, что sine 30{\degree}30° равен 1/2.
А cosine 30{\degree}30° равен √3/2.
Теперь, давайте решим уравнения, чтобы найти SH и HB.
1/2 = SH / 5 => SH = 5/2
√3/2 = HB / 5 => HB = (5√3)/2
Теперь у нас есть значения противолежащего катета SH = 5/2 и прилежащего катета HB = (5√3)/2.
Чтобы найти тангенс угла θθ, нам нужно подставить значения SH и HB в уравнение тангенса:
Тангенс угла θθ = SH / HB = (5/2) / ((5√3)/2)
Теперь мы можем упростить это уравнение:
Тангенс угла θθ = (5/2) * (2 / (5√3)) = 1/√3 = √3/3
То есть, тангенс угла θθ равен √3/3.
Окончательный ответ: Тангенс угла между прямой SASA и плоскостью SBCSBC равен √3/3.