1. Геометрия
  2. Из точки , не принадлежащей

Из точки , не принадлежащей данной плоскости, проведены к ней две наклонные , равные 10 см и 18 см. сумма длин их проекций на плоскость равна 16 см.найти проекцию каждой наклонной

swetakorchagov swetakorchagov    3   30.03.2019 18:20    18

Ответы
PomoGayka0 PomoGayka0  27.05.2020 18:22

AB=10, BC=18, AC=16, AK - проекция АВ, КС - проекция ВС, следовательно угол ВКС прямой.

Пусть АК=х, тогда СК=16-х

Из прямоуг. тр. ABK по т. Пиф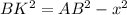 BK^2=AB^2-x^2 и из прямоуг. треуг. ВКС 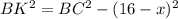BK^2=BC^2-(16-x)^2. Значит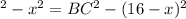  АВ^2-x^2=BC^2-(16-x)^2

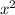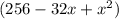
100-x^2=324-(256-32x+x^2)

0=224-256+32x

32x=32

x=1. Проекция АВ = 1, тогда проекция ВС=16-1=15


Из точки , не принадлежащей данной плоскости, проведены к ней две наклонные , равные 10 см и 18 см.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
jsjdn jsjdn  16.09.2019 07:20
Вправильной четырёхугольной пирамиде pabcd с ребром 1 точка q - центр основания, а точка k - середина pc. вычислите длину перпендикуляра: а) из k на (abc); б) из k на...
MintSuga MintSuga  05.08.2019 10:20
Чи можна побудувати ромб з висотою 5 см і однією з діагоналей що дорівнює 6 см...
GrechukhinGleb GrechukhinGleb  05.08.2019 10:20
Найдите углы, образованные при пересечении двух прямых , если разность двух из них равна 64 градуса...
ppapsd ppapsd  05.08.2019 10:20
Знайдіть суміжні кути, якщо один із них на 20° менше, ніж другий. подскажите как решить)...
Roflobara Roflobara  05.08.2019 10:20
Чи можуть точки a; b; c; лижати на одній прямій якщо ab=1,8ь; ac=1,3м; bc=3 м...
pinelike pinelike  05.08.2019 10:10
Луч oc проходит между сторонами угла aoe.луч ob-биссиктриса угла aoc,луч od-биссиктриса угла coe.найдите угол bod, если угол aoe=144°...
GlebRyabov GlebRyabov  05.08.2019 10:10
Abcd диагонали прямоугольника на точке 0 пересекаются.если cad=30°,ac=12 см,то найдите периметр треугольника aob....
IrinaEfremova2003 IrinaEfremova2003  05.08.2019 10:10
Кут b на 18 більший від кута а.знайти кути паралелограма....
Незнакомец134 Незнакомец134  05.08.2019 10:10
Вравнобедренном треугольнике abc с основанием ab=8 м проведена медиана ad. p треуг.acd-p треуг.abd=2м.найти ac....
DirolFix DirolFix  05.08.2019 10:10
Вчетырёхугольной пирамиде все боковые рёбра наклонены к плоскости основанию под углом 60градусов. из основания где лежит равнобедренная трапеция большой угол которой...

Популярные вопросы