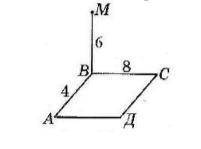
Из точки М проведен перпендикуляр к плоскости прямоугольника АВСД (рис. 3). Найдите расстояние от М до сторон прямоугольника АВСД, если известно, что МВ = 6см, ВС = 8см, АВ = 4 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Знайди градусну міру кута між стрілками годинника, якщо він показує:...
2 - 3 вершини прямого кута проведено промінь так, що він ділить прямий...
1 - Прямий кут АОВ поділено променями ОМ і ОК Гак, що ∟AOK = 63°, a ∟BOM...
2 - Накресли кут АОВ, градусна міра якого 60°. За до транспортира проведи...
1 - Запиши всі натуральні числа, які лежать на координатному промені між...
3 - Знайди кут між бісектрисою і стороною даного кута, що дорівнює: 1)...
3 - Кут МОК у три рази менший від кута KON (рис. 134). Знайди ці кути,...
1 - Знайди градусну міру кута та визнач його вид, ікщо бісектриса кута...
1 - Розгорнутий кут COD поділено променями ON і ОК так, що ∟DON = 130°,...
3 - Промінь ON ділить кут АОВ на два кути: AON і NOB. Знайди градусну міру...
1
Дано: МВ = 6 см, ВС = 8 см, АВ = 4 см.
Первым шагом нам нужно понять, какие стороны прямоугольника будут соединены с точкой М.
Из рисунка видно, что точка М соединена с точками В и С. Поэтому нам нужно найти расстояние от М до сторон ВС и ВА.
Для начала, посмотрим на треугольник МВС. В этом треугольнике нам известны все три стороны. Вспомним, что если в прямоугольном треугольнике известны две катеты, то мы можем найти гипотенузу с помощью теоремы Пифагора.
Таким образом, найдем МС, которая является гипотенузой этого треугольника:
МС² = МВ² + ВС²
МС² = 6² + 8²
МС² = 36 + 64
МС² = 100
МС = √100
МС = 10 см
Теперь нам нужно найти расстояние от точки М до стороны АВ. Обратимся к треугольнику МАВ.
Расстояние от точки М до стороны АВ будет равно высоте прямоугольника АВСД, поскольку М проведена перпендикулярно плоскости прямоугольника.
Теперь обратимся к треугольнику МВС. В нем МС - это гипотенуза, а сторонами треугольника являются МВ и ВС.
Мы уже знаем, что МС = 10 см, МВ = 6 см и ВС = 8 см.
Теперь применим теорему Пифагора, чтобы найти МА:
МА² = МВ² - АВ²
МА² = 6² - 4²
МА² = 36 - 16
МА² = 20
МА = √20
МА = 2√5 см
Таким образом, расстояние от точки М до стороны АВ прямоугольника АВСД составляет 2√5 см, а расстояние от точки М до стороны ВС составляет 10 см.
По телреме о трех перемен
Хвзввзвээв