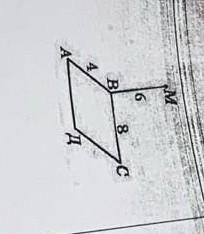
Из точки M проведен перпендикуляр к плоскости АВСД. Найдите расстояние от М до сторон прямоугольника АВСД

Чтобы найти расстояние от точки М до сторон прямоугольника АВСД, мы можем воспользоваться свойством перпендикуляров.

Для начала обозначим точки на плоскости АВСД. Вершины прямоугольника обозначим как A, B, C и D. Обозначим середину стороны АВ как P, а середину стороны СD как Q.

Затем проведем от точки М перпендикуляры к линиям AB, BC, CD и DA. Пусть точки пересечения этих перпендикуляров с соответствующими сторонами прямоугольника обозначены как E, F, G и Н, соответственно.

Чтобы найти расстояние от точки М до стороны AB, мы можем воспользоваться теоремой Пифагора. Расстояние от М до стороны AB равно длине отрезка ME. Так как треугольник AME прямоугольный, мы можем найти его длину, используя теорему Пифагора:

ME = √(AM^2 - AE^2).

Аналогично, расстояние от точки М до стороны BC равно длине отрезка MF, расстояние от точки М до стороны CD равно длине отрезка MG, и расстояние от точки М до стороны DA равно длине отрезка MH.

Чтобы найти длины отрезков AE, BF, CG и DH, мы можем использовать свойство параллелограмма. Поскольку линия МЕ перпендикулярна к стороне АB, а сторона АВ параллельна стороне CD, мы можем заключить, что длина отрезка ME равна длине отрезка AQ, а длина отрезка AE равна длине отрезка QP.

Таким образом, мы можем использовать теорему Пифагора, чтобы найти длины отрезков AE, BF, CG и DH:

AE = √(AQ^2 - QP^2),
BF = √(BP^2 - QP^2),
CG = √(CQ^2 - QP^2),
DH = √(DQ^2 - QP^2).

Используя найденные значения AE, BF, CG и DH, мы можем подставить их в теорему Пифагора, чтобы найти расстояния от точки М до каждой из сторон прямоугольника:

ME = √(AM^2 - AE^2),
MF = √(BM^2 - BF^2),
MG = √(CM^2 - CG^2),
MH = √(DM^2 - DH^2).

Все эти значения будут представлять расстояния от точки М до каждой из сторон прямоугольника АВСД.