Из точки м проведён перпендик.md=4см.к плоскости прямоуг. abcd наклонные ма и мс образуют плоскости треуг. угол45и 30 соответст. найти стороны прямоуг.

не уверена, что это правильно, но...)

треуг.ADM - п/у т.к. MD - перп. плоскости); треуг. ADM - р/б (т.к. Угол МАС=45гр.)

Следовательно DM=AD=4.

угол MCD=30гр. следовательно MD=1/2MC

MC=8

CD=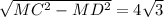

Прямая MD перпендикулярна к плоскости, а знасин она перп к любой прямой лежащей в этой плоскости(по определению перпен. прям и плоск.). Значит треугольники AMD и MDC-прямоугольные.

Рассмотрим треуг. MDC.MD=4, а угол MDC=30град.Катет, лежащий против угла в 30град=половине гипотенузы; следовательно MC=8.И по Пифагору находим сторону DC прямоугольника.Она = 4√3.

Далее рассмотрим треуг. AMD.Угол MAD=45град., значит треугольник равнобедреный,и сторона AD прямоугольника тоже = 4.

ответ:стороны прямоугольника равны 4 и 4√3.

Блин опаздала чуть чуть...:)

даже жалко...

все равно один хрен-задача легкая