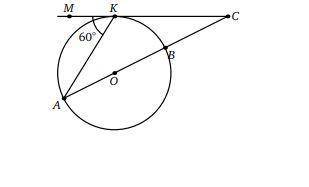
Из точки C проведена касательная CK к окружности с центром O. На продолжении отрезка CK за точку K отмечена точка M. Окружность пересекает отрезок CO в точке B, а его продолжение — в точке A. Известно, что ∠AKM = 60 и AB=11. Найдите AC. ответ должен быть 16,5.
Другие вопросы по теме Геометрия
Популярные вопросы
- Перевидите: match the clubs and the students stories и - rewrite...
1 - Экзамен по , второй курс. нужны именно решения, а не ответы. буду...
2 - Имеются помидоры огурцы лук сколько различных салатов можно приготовить...
1 - Подобрать однокоренные слова с корнем -кот,,друг,гриб...
2 - Вцепи имеется блок, состоящий из трех последовательно соединенных...
1 - Площадь сечения куба представляющего собой правильный шестиугольник...
3 - Сторона основания правильного четырёхугольной пирамиды равна 6 см,...
1 - Скаласти речення з словом не здужати пліз ! : -)...
2 - Наш школьный психолог спросил: оно справедливее богов, но коварнее...
3 - Скласти діалог на тему як досягти авторитер серед одноліток...
2
16.5
Объяснение:
AOK
OK=AO радиусы
Значит АОК равнобедренный
<ОКС=90° (радиус и касательная)
<АКО=180-90-60=30°
<АКО=<КАО=30°
<КАО=дуга BK/2 (так как угол опирается на эту дугу)
BK=<KOC
<KOC=2*KAO=60
KOC прямоугольный
<КСО=90-60=30
sinKCO=KO/OC=sin30=1/2
OC =KO*2= 5.5*2=11
AC=OC+AO=11+5.5=16.5