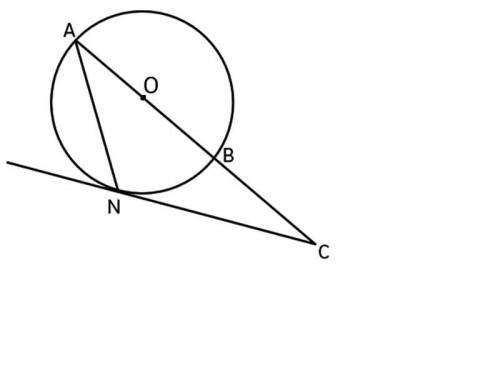
Из точки C, которая лежит вне окружности, проведена секущая AC, проходящая через центр окружности, и касательная CN. Найдите градусную меру меньшей дуги BN, если угол ANC = 120°.

Для того чтобы решить эту задачу, нам потребуется использовать несколько свойств окружностей и треугольников. Давайте разберем ее по шагам. Шаг 1: Поскольку угол ANC = 120°, а угол между касательной и радиусом, проведенным из точки касания, всегда равен 90°, то угол ANB = 360° - 120° - 90° = 150°. Таким образом, меру угла ANB мы уже нашли. Шаг 2: Так как AC - секущая, проходящая через центр окружности, то для любых двух точек на окружности секущая будет делить между собой дугу окружности на равные части. Следовательно, дуга AB также делится секущей AC на две равные дуги. Это значит, что дуга BN имеет такую же градусную меру, как и дуга BAC. Шаг 3: Поскольку дуга BAC делится секущей AC на две равные части, то мера дуги BAC равна половине меры дуги ABC. Да бы найти меру дуги ABC, нам нужно воспользоваться свойством, согласно которому центральный угол окружности равен половине меры дуги, заключенной между его сторонами. Шаг 4: Обратим внимание, что угол ABC - это центральный угол, поскольку его стороны проходят через центр окружности. Следовательно, мера дуги ABC равна удвоенной мере угла ABC. Мера угла ABC равна 180° - 120° (120° получается из того, что угол ANC = 120°, и угол ABC и угол ANC являются смежными). Шаг 5: Подставляем значения: мера угла ABC = 180° - 120° = 60°. Таким образом, мера дуги ABC равна удвоенной мере угла ABC, то есть 2 * 60° = 120°. Ответ: Меньшая дуга BN имеет градусную меру 120°.