1. Геометрия
  2. Из основания высоты правильной

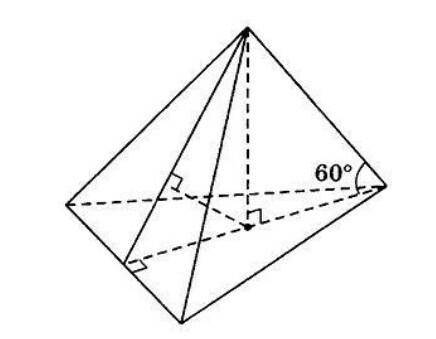
Из основания высоты правильной треугольной пирамиды опущен перпендикуляр длиной 1 на боковую грань. Найдите объём пирамиды, если боковое ребро составляет с плоскостью основания угол 60°.​


Из основания высоты правильной треугольной пирамиды опущен перпендикуляр длиной 1 на боковую грань.

giunel041 giunel041    3   26.03.2021 19:40    9

Ответы
MishkaBra MishkaBra  25.04.2021 20:49

\boldsymbol{\dfrac{13\sqrt{39}}{12}}

Объяснение:

Пирамида правильная, значит в основании правильный треугольник, О - центр вписанной и описанной окружности.

Пусть сторона основания - а.

OH=\dfrac{a\sqrt{3}}{6} как радиус окружности, вписанной в основание.

OB=\dfrac{a\sqrt{3}}{3} как радиус окружности, описанной около основания.

ΔSOB:

   \dfrac{SO}{OB}=tg60^\circ

SO=OB\cdot tg60^\circ=\dfrac{a\sqrt{3}}{3}\cdot \sqrt{3}=a

ΔHSO: по теореме Пифагора

SH=\sqrt{SO^2+OH^2}=\sqrt{a^2+\dfrac{3a^2}{36}}=\sqrt{\dfrac{39a^2}{36}}=\dfrac{a\sqrt{39}}{6}

Высота прямоугольного треугольника с катетами a и b  и гипотенузой с:

h=\dfrac{ab}{c}

Из прямоугольного треугольника HSO:

OK=\dfrac{SO\cdot OH}{SH}=\dfrac{a\cdot\frac{a\sqrt{3}}{6}}{\frac{a\sqrt{39}}{6}}=\dfrac{a\cdot\sqrt{3}\cdot 6}{6\cdot a\sqrt{39}}=\dfrac{a}{\sqrt{13}}

OK = 1

\dfrac{a}{\sqrt{13}}=1

a=\sqrt{13}

Площадь основания:

S=\dfrac{a^2\sqrt{3}}{4}=\dfrac{13\sqrt{3}}{4}

V=\dfrac{1}{3}S\cdot SO

V=\dfrac{1}{3}\cdot \dfrac{13\sqrt{3}}{4}\cdot \sqrt{13}=\boldsymbol{\dfrac{13\sqrt{39}}{12}}


Из основания высоты правильной треугольной пирамиды опущен перпендикуляр длиной 1 на боковую грань.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
21ololoha 21ololoha  01.08.2019 22:00
Найти параллельные прямые или отрезки и доказать их параллельность....
sowaties sowaties  01.08.2019 22:00
Один из внешних углов равнобедренного треугольника равен 70 градусов. найдите углы треугольника...
BafuDzn BafuDzn  01.08.2019 22:00
Периметр четырехугольника равен 80 см. егор первая сторона больше второй на 10 см и на столько же меньше третьей стороны, а четвертая в 2 раза больше второй стороны. найдите стороны...
lime89cc lime89cc  11.09.2019 00:20
Выпиши из словарика 10 слов с нулевым окончанием...
дочь20 дочь20  11.09.2019 00:20
Які існують види трикутників залежно від кількості рівних сторін? ! !...
MUSIC555 MUSIC555  08.02.2021 05:26
1.Докажите, что MNPQ равнобокая трапеция, если...
SaSeRoS SaSeRoS  08.02.2021 05:38
Отметьте точки A (4; -2) и B (-3; 4) в системе координат и найдите расстояние AB.​...
YomiTan YomiTan  08.02.2021 05:41
Найдите высоту диаметра цилиндра, образованного прямоугольником со сторонами 6 и 10 сантиметров.​...
Bois123543 Bois123543  21.06.2019 17:20
Найдите отношение отрезков mn и cd, если их длины равны соответственно 10 см и 2 см. !...
Tim4ik0205 Tim4ik0205  15.08.2019 10:00
Серединный перпендикуляр стороны ас треугольника авс проходит черезвершину в. найдите угол с, если угол а =17 градусов....

Популярные вопросы