из одной точки к прямой проведено две наклоные. ода из них в длинну 24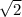см образует с прямой угл 45°. найдите длинну другой наклонной, если её проекция на прямой равна 18 см. ​

Пусть из точки А проведено две наклонные АВ И АС, ∠АВС=45°, значит, в равнобедренном ΔАВК/т.к. углы при основании равны, то он равнобедренный, по признаку/, АК=ВК=х, тогда х²+х²=(24√2)², 2х²=24²*2, т.к. х-положительно, то х = 24, и из ΔАКС наклонная АС равна

√АК²+КС²=√24²+18²=√900=30(см)

ответ:30 см.

Удачи.