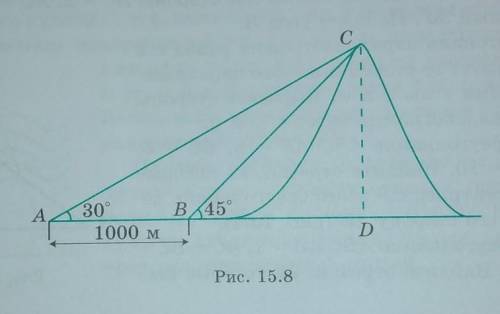
Из некоторой точки вершина горы видна под углом 30°. При приближении к горе на 1000м вершина стала видна под углом 45°. Найдите приблизительную высоту горы. В ответе укажите целое число метров ​

Добрый день, дорогой ученик!

Для того чтобы решить эту задачу, нам потребуется использовать геометрические знания, а именно теорему синусов.

Перед тем как начать, давай разберемся с построением:



Здесь у нас есть треугольник ABC, в котором AB - гора, BC - расстояние от наблюдателя до горы, а AC - расстояние, на которое приблизился наблюдатель к горе.

Из условия задачи известно, что угол A равен 30 градусам, а угол B равен 45 градусам. Также дано, что при приближении к горе на 1000м угол B стал равным 45 градусам.

Теперь мы можем приступить к решению задачи.

1. Используя теорему синусов, найдем отношения сторон треугольника ABC:
sin(A) = AB / BC
sin(B) = AC / BC

2. Подставим значения углов и расстояний в соответствующие уравнения:
sin(30) = AB / BC
sin(45) = (AC + 1000) / BC

3. Решим получившуюся систему уравнений для нахождения значений AB и BC.

Из первого уравнения получим:
AB = BC * sin(30)

Подставим это значение во второе уравнение:
sin(45) = (AC + 1000) / (BC * sin(30))

4. Решим получившееся уравнение относительно AC:
sin(45) = (AC + 1000) / (BC * (1/2))
sin(45) = (AC + 1000) / (BC / 2)
sin(45) = 2(AC + 1000) / BC
(√2)/2 = (AC + 1000) / BC

Теперь можем найти AC:
(√2)/2 * BC = AC + 1000
(√2)/2 * BC - 1000 = AC

5. В ответе нужно указать целое число метров. Заметим, что BC при приближении к горе увеличилось на 1000 м. Поскольку нам нужно найти высоту горы, которую обозначим через h, то ее значение можно получить, вычтя из BC этот сдвиг на 1000 м: BC - 1000.

Подставим это значение в получившуюся формулу для AC:
(√2)/2 * (BC - 1000) - 1000 = AC

Раскроем скобки:
(√2)/2 * BC - (√2)/2 * 1000 - 1000 = AC

(√2)/2 * BC - (√2)/2 * 1000 - 1000 - AC = 0

Таким образом, высота горы составляет (√2)/2 * BC - (√2)/2 * 1000 - 1000 метров.

Ответ: (√2)/2 * BC - (√2)/2 * 1000 - 1000 метров.

Надеюсь, ответ был понятен и помог вам разобраться с задачей! Если возникнут еще вопросы, обращайся!