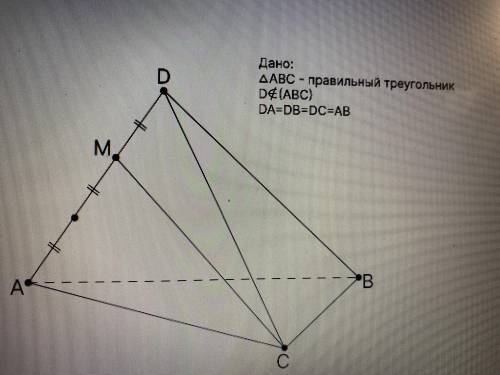
Исходя из данных рисунка, найти квадрат косинуса угла между прямыми CM и AB. Результат округлить до сотых
Другие вопросы по теме Геометрия
Популярные вопросы
- Процессоры істен шыққан компьютер жұмыс істей ме?...
1 - Б) Диагональ прямоугольного параллелепипеда с квадратным основанием...
3 - ВПР. Русский язык. 5 класс. Вариант 2 Выпишите предложение , в котором...
3 - Решите неравенство(х+1)(х+2)^2 =0(х^2-6х+9)(х-2) =0(х^2-3х+2)(х^2-4)...
1 - 5толстых и 5 тонких вопросов на расказ солдатёнок Ч.Т.Айматов...
1 - Б) Треугольник, изображённый на рисунке б, дострой до квадрата с циркуля...
2 - не особо понимаю алгебру ...
3 - Подготовить рассказ о казахско...
3 - Життя селян у 16 столітті на україні ...
1 - Менің сөйлеу мәдениетім эссе тез керек...
1
1. Обозначим угол между прямыми CM и AB как α.
2. По свойству перпендикулярных прямых, угол α равен углу МСD.
3. По свойству вертикальных углов, угол МСD также равен углу КРА.
4. Обратим внимание, что угол КРА является противолежащим углом по отношению к стороне KM. Поэтому, мы можем использовать теорему косинусов для нахождения квадрата косинуса угла КРА.
5. Теорема косинусов гласит: c^2 = a^2 + b^2 - 2ab*cos(C), где c - длина стороны, противолежащей углу C, a и b - длины двух других сторон треугольника.
6. Обозначим длины сторон треугольника КМC как a, b и c. Тогда, a = KM, b = CR и c = KC.
7. Мы знаем, что KM = 6, CR = 12 и KC = 10 (по данным на рисунке).
8. Подставим полученные значения в формулу теоремы косинусов и найдем квадрат косинуса угла α:
KC^2 = KM^2 + CR^2 - 2*KM*CR*cos(α)
10^2 = 6^2 + 12^2 - 2*6*12*cos(α)
100 = 36 + 144 - 144*cos(α)
0 = 36 - 144*cos(α)
cos(α) = 36/144
cos(α) = 0.25
9. Теперь найдем квадрат косинуса угла α, чтобы округлить результат до сотых. Квадрат косинуса угла α равен cos^2(α), поэтому:
cos^2(α) = 0.25^2 = 0.0625
10. Ответ: квадрат косинуса угла α между прямыми CM и AB равен 0.0625 (округлено до сотых).