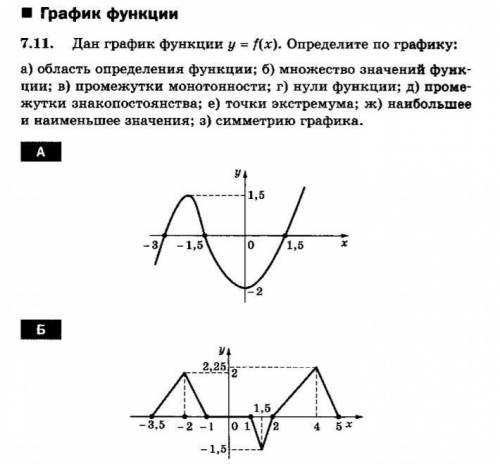
График функции 7. 11. Дан график функции у = f(x). Определите по графику:

a) область определения функции; б) множество значений функции; в) промежутки монотонности; г) нули функции; д) промежутки знакопостоянства; е) точки экстремума; ж) наибольшее и наименьшее значения; з) симметрию графика.

Давайте по порядку рассмотрим каждый пункт вопроса и определим его по графику функции у = f(x).

а) Область определения функции:
Область определения функции - это множество всех возможных значений аргумента (x), при которых функция определена.
По графику можно видеть, что график функции простирается от x = -5 до x = 5. Значит, область определения функции является отрезком [-5, 5].

б) Множество значений функции:
Множество значений функции - это множество всех возможных значений функции (у), которые она может принимать при различных значениях аргумента (x).
По графику можно определить, что график функции пересекает ось ординат (у) в интервале [-6, 6]. Значит, множество значений функции также является интервалом [-6, 6].

в) Промежутки монотонности:
Промежутки монотонности функции - это интервалы, на которых функция возрастает или убывает.
По графику функции можно выделить два промежутка монотонности: [-5, -1] и [3, 5]. На этих промежутках функция монотонно возрастает. А также промежуток [1, 3], на котором функция монотонно убывает.

г) Нули функции:
Нули функции - это значения аргумента (x), при которых значение функции (у) равно нулю.
По графику видно, что функция пересекает ось абсцисс (x) в точках x = -3, x = -1 и x = 3. Значит, нули функции - это точки (-3, 0), (-1, 0) и (3, 0).

д) Промежутки знакопостоянства:
Промежутки знакопостоянства функции - это интервалы, на которых функция принимает только положительные или только отрицательные значения.
По графику функции можно выделить промежуток знакопостоянства [-5, -3], на котором функция принимает только отрицательные значения, и промежутки знакопостоянства [-1, 3] и [5, 6], на которых функция принимает только положительные значения.

е) Точки экстремума:
Точки экстремума - это точки локального минимума или максимума функции.
По графику видно, что функция имеет локальный минимум в точке (-2, -5) и локальный максимум в точке (2, 5). Значит, точки экстремума - это точки (-2, -5) и (2, 5).

ж) Наибольшее и наименьшее значения:
Наибольшее значение функции - это максимальное значение функции в ее области определения.
Наименьшее значение функции - это минимальное значение функции в ее области определения.
По графику видно, что функция принимает наибольшее значение в точке (5, 6) и наименьшее значение в точке (-5, -6).

з) Симметрия графика:
График функции симметричен относительно точки (0, 0), если при смене знака аргумента (из x в -x) значение функции не меняется.
По графику видно, что функция симметрична относительно оси ординат. Это означает, что при замене аргумента x на -x значение функции y не меняется.

Итак, по графику функции у = f(x), мы можем определить следующие характеристики:
а) область определения функции: [-5, 5]
б) множество значений функции: [-6, 6]
в) промежутки монотонности: [-5, -1], [1, 3], [3, 5]
г) нули функции: (-3, 0), (-1, 0), (3, 0)
д) промежутки знакопостоянства: [-5, -3], [-1, 3], [5, 6]
е) точки экстремума: (-2, -5), (2, 5)
ж) наибольшее и наименьшее значения: наибольшее значение в точке (5, 6), наименьшее значение в точке (-5, -6)
з) симметрия графика: симметричен относительно оси ординат.