Гипотенуза прямоугольного треугольника равна 14см,а сумма длин катетов равна 19,6см. найти длину каждого катета.

Ответы

tolodono 21.08.2020 21:17

Обозначим стороны треугольника через a, b и с. Пусть a и b - катеты прямоугольного треугольника, с - его гипотенуза.

Тогда задачу можно свести к решению системы из двух уравнений. Одно из них - теорема Пифагора, второе сумма длин катетов.

$\begin{cases}a^2 + b^2 = 14^2,\\a + b = 19,6.\end{cases}$

Выразим из второго уравнения переменную b.

$\begin{cases}a^2 + b^2 = 14^2,\\b = 19,6 - a.\end{cases}$

Подставим второе уравнение в первое.

$a^2 + (19,6 - a)^2 = 14^2;\\a^2 + 19,6^2 - 2\times 19,6a + a^2 - 14^2 = 0;\\2a^2 - 2\times 19,6a + (19,6^2 - 14^2) = 0;\\2a^2 - 2\times 19,6a + (19,6 - 14)(19,6 + 14) = 0;\\2a^2 - 2\times 19,6a + 5,6\times 33,6 = 0;\\a^2 - 19,6a + 94,08 = 0;\\D = \big[b^2 - 4ac\big] = (-19,6)^2 - 4\times 94,08 = 7,84 = 2,8^2;\\a_{1,2} = \left[\dfrac{-b\pm\sqrt{D}}{2a}\right] = \dfrac{19,6\pm2,8}{2} = 9,8\pm1,4.\\\left[\begin{array}{c}a_1 = 9,8 - 1,4 = 8,4,\\a_2 = 9,8 + 1,4 = 11,2.\end{array}\right$

Подставляем полученные значения во второе уравнения.

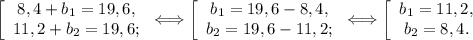
$\left[\begin{array}{c}8,4 + b_1 = 19,6,\\11,2 + b_2 = 19,6;\end{array}\right\Longleftrightarrow \left[\begin{array}{c}b_1 = 19,6 - 8,4,\\b_2 = 19,6 - 11,2;\end{array}\right\Longleftrightarrow \left[\begin{array}{c}b_1 = 11,2,\\b_2 = 8,4.\end{array}\right$

На выходе имеем два решения: a = 8,4 см; b = 11,2 см.a = 11,2 см; b = 8,4 см.ответ: 8,4 см и 11,2 см; 11,2 см и 8,4 см.