Геометрия Задание 1.
Дан параллелепипед АВСD А1, В1, С1: D1. Компланарны ли вектора: АВ, АD, АА, -
Задание 2. Дан параллелепипед АВСD А1, В1.С1, D1;. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов:
а) АВ + АD+ АА1,,
б)DА + DС + DD1.
Задание 3. В тетраэдре АВСО медиана АА1; грани АВС делится точкой К так, что АК: КА1; = 3:7,
Разложите вектор DК по векторам DА, DВ, DС.
Заданне 4. Отрезки АВ и СD не лежат в одной плоскости, точки М и N— середины этих отрезков. Докажите, что МN
Задание 5. Отрезки, соединяющие середины противоположных сторон четырехугольника АВСD, пересекаются в точке М. Точка О — произвольная точка пространства. Докажите, что справедливо равенство ОМ =
Задание 6. На трех некомпланарных векторах p = АВ, q= АD, r = АА1, построен параллелепипед АВСD А1,В1,С1,D1. Разложите по векторам р,q,r векторы, образованные диагоналями этого параллелепипеда
- Задание 7. Векторы a и b, b и c коллинеарны. Докажите, что коллинеарны векторы 3a + 2c и b.
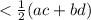
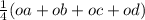
Ответы
Показать ответы (3)
Другие вопросы по теме Геометрия
Популярные вопросы
- Резистори, опори яких 2кОм і 3 кОм, з єднані паралельно і підключенні до джерела...
2 - У зошиті з української літератури вам необхідно придумати та написати власну історію...
1 - Назовите итоги Реформации1.2.3.4.5....
3 - Отдых. Текст. Связь предложений в тексте. Урок 2 3 ЗАДАНИЕ ОНЛАЙН МЕКТЕП...
1 - укажіть якою буде температура повітря на вершині гори, якщо біля її підніжжя температура...
2 - До іть будь ласка ів, будь ласка❤...
3 - 9 Что из перечисленного находится в мозговом слое почки? а) Петля нефрона и собирательная...
1 - 8. Исключи лишнее 1Катaлaунская битва2контрибуция3папа Римский4бек...
1 - Как построено стихотворение Лермонтова Русалка . Сколько в нем частей. сколько...
2 - ЛЮДИ, ЭТО , СОР ПО МАТЕШЕ15Б + ЛУЧШИЙ ОТВЕТ...
1