ГЕОМЕТРИЯ, СМОТРИТЕ КАРТИНКУ

См. Объяснение

Объяснение:

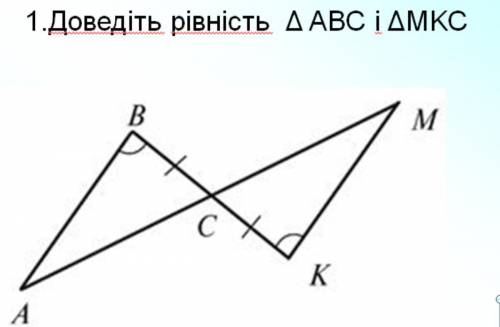
Треугольник АВС равен треугольнику МКС, так как:

1) сторона ВС треугольника АВС равна стороне СК треугольника МКС - согласно условию;

2) угол ВСА треугольника АВС, прилежащий к стороне ВС, равен углу МСК, прилежащему как стороне СК треугольника МКС , - как углы вертикальные;

3) угол В, прилежащий к стороне ВС треугольника АВС, равен углу К прилежащему как стороне СК треугольника МКС - согласно условию.

Если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Следовательно, ΔАВС = ΔМКС, - что и требовалось доказать.