Геометрия. С 6 по 8 задание Номер 7: a || B, CD = 56, AC BD= M,
AM: AC=3:4. Найдите АВ.
Номер 8: a || B. AB NCD=0, BD=8,
AO: AB=3: 5. Найдите АС.
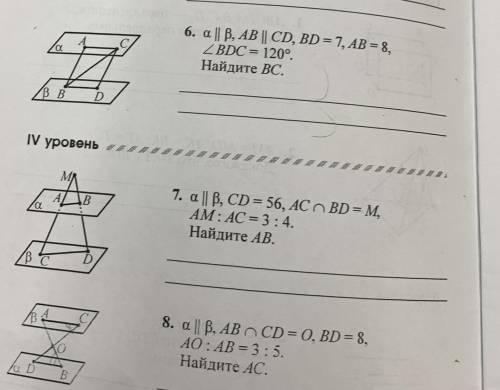
Другие вопросы по теме Геометрия
Популярные вопросы
- Раб адальберт, принадлежавший сацебарону франкского королевства гильденбранту,...
1 - 5. перепишите предложения, вставляя данные в скобках глаголы в 3-емлпце...
3 - Определи, какие высказывания относятся к элементу, а какие — к веществу:...
2 - Мотивы искушения, мотивы своеволия и свободы в драме гроза островского....
3 - 15 8 класс (часть 2) 21. назовите год, когда россия установила дипломатические...
2 - Определить величину и направление реакции связи...
3 - Найди в тексте слова и словосочетания, которые соответствуют толкованиям...
1 - Рыба паровая,рыба тельная, рыба заливная ,страгонина...
3 - Приводите обыкновенные дроби 1/2,2/3,4/7,5/14,8/21,1/6-кобыуновенной...
2 - Выразите в метрах и запишите в виде десятичной дроби 3м 5дм 4см. завтра...
1
Номер 7:
Мы имеем данный факт: отрезок CD равен 56 единицам.
Также известно, что линия a параллельна линии B.
Мы знаем, что AM:AC = 3:4, что означает, что отношение длины отрезка AM к длине отрезка AC равно 3:4.
Нам нужно найти длину отрезка AB.
Чтобы решить эту задачу, нам понадобится использовать свойство параллельных линий, которое гласит, что соответственные углы при пересечении линий a и B равны.
Таким образом, у нас есть два подобных треугольника: треугольник AMD и треугольник ACB. Они подобны по причине того, что у них одинаковые углы, так как линии a и B параллельны.
Также у них соответствующие стороны пропорциональны. Мы знаем, что AM:AC = 3:4, поэтому мы можем предположить, что пропорциональность также будет верна для сторон DM и CB.
Поэтому мы можем записать следующую пропорцию:
DM:CB = AM:AC = 3:4
Мы знаем, что CD = 56, а DM + MC = CD. Так как AM и CB - это соответствующие стороны треугольников AMD и ACB, а стороны AM и CB пропорциональны сторонам DM и MC, мы можем записать следующие пропорциональные уравнения:
DM/MC = AM/AC = 3/4
DM + MC = CD
Подставим известные значения:
DM/MC = 3/4, CD = 56
Теперь мы можем решить эти уравнения:
DM/MC = 3/4
4DM = 3MC
DM = (3/4)MC
DM + MC = CD
(3/4)MC + MC = 56
(7/4)MC = 56
MC = (4/7)*56
MC = 32
Теперь, чтобы найти длину AB, мы можем использовать пропорцию AM:AC = AB:CB:
AM/AC = AB/CB
3/4 = AB/(32+CB)
3/4 = AB/(32+AB/3)
3/4 = AB/(96+AB)/3
3/4 = 3AB/(96+AB)
12 = 3AB
AB = 12/3
AB = 4
Таким образом, длина AB равна 4.
Номер 8:
Мы сталкиваемся с аналогичной задачей.
Мы знаем, что AB || CD.
Мы также знаем, что отношение AO к AB равно 3:5.
Нам нужно найти длину AC.
Мы можем использовать подобные методы для решения этой задачи.
Опять же, мы имеем два подобных треугольника: треугольник AOD и треугольник ACB. Они имеют одинаковые углы, так как линии AB и CD параллельны.
Мы также знаем, что AO:AB = 3:5, что означает, что стороны AD и CB также пропорциональны.
Мы можем записать пропорцию:
AD/CB = AO/AB = 3/5
Мы знаем, что BD = 8, и нам нужно найти AC. Мы также знаем, что AD + DC = AC.
Мы можем использовать те же пропорциональные уравнения, что и в предыдущей задаче:
AD/CB = 3/5
3CB = 5AD
CB = (5/3)AD
AD + DC = AC
AD + 56 = AC
Подставим известные значения и решим уравнения:
(5/3)AD + AD = 8 + AD + 56
(8/3)AD = 64
AD = (3/8)*64
AD = 24
Теперь мы можем использовать пропорцию AO:AB = AD:AC, чтобы найти длину AC:
3/5 = 24/AC
3AC = 5*24
3AC = 120
AC = 120/3
AC = 40
Таким образом, длина AC равна 40.
Надеюсь, это решение помогло вам понять поставленные задачи по геометрии. Если у вас возникнут еще вопросы, пожалуйста, свяжитесь со мной.