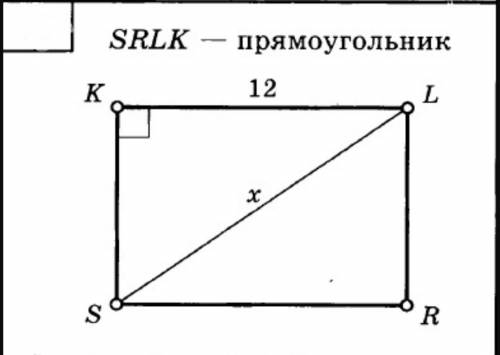
Геометрия. Найдите х (сторону SL)

Добрый день! Давайте решим данный геометрический вопрос. У нас есть треугольник ABC.

Сначала посмотрим на прямые AC и SL. Мы видим, что они параллельны, так как они обе пересекаются с прямой AB.

Теперь, когда у нас есть две параллельные прямые (AC и SL), мы можем использовать теорему о параллельных линиях. Эта теорема говорит о том, что если две параллельные прямые пересекают пересекающиеся прямые (в данном случае AB и SL), то соответственные углы равны.

Смотрим на углы: угол BAC и угол ASL. Они соответствующие углы, так как линия AC является пересекающей, и они находятся на одной стороне от этой линии.

Мы знаем, что угол BAC равен 60 градусов (это указано на рисунке). Исходя из теоремы о параллельных линиях, угол ASL также будет равен 60 градусам.

Теперь давайте сосредоточимся на треугольнике ASL. Мы знаем, что угол ASL равен 60 градусам, и угол S равен 90 градусам, так как это прямой угол.

Итак, у нас есть два угла треугольника ASL. Сумма углов в треугольнике всегда равна 180 градусам.

Чтобы найти третий угол, нам нужно вычесть сумму углов ASL и S из 180 градусов:

180 - 60 - 90 = 30.

Таким образом, угол L равен 30 градусам.

Теперь мы можем использовать теорему синусов для нахождения стороны SL. Теорема синусов утверждает, что отношение длины стороны к синусу противолежащего ей угла в треугольнике равно для всех трех сторон треугольника.

Давайте обозначим сторону SL как х. У нас есть угол L, который равен 30 градусам. Таким образом, мы можем записать пропорцию:

х / sin(30) = AB / sin(90).

sin(90) равно 1, так как синус прямого угла равен 1.

Следовательно, пропорция может быть упрощена до:

х = AB / sin(30).

Осталось только определить длину стороны AB и вычислить значение sin(30).

По рисунку мы видим, что AB равно 20.

Значение sin(30) можно найти в таблице значений тригонометрических функций.

Подставим все значения в формулу:

х = 20 / sin(30) = 20 / 0.5 = 40.

Таким образом, сторона SL равна 40 единицам.

Надеюсь, это пояснение помогло вам понять задачу и ее решение. Если возникнут еще вопросы, не стесняйтесь задавать!"