Геометрия, Файл как можно быстрее, умоляю, С РЕШЕНИЕМ

Для решения данной геометрической задачи, мы можем воспользоваться основным свойством пересекающихся хорд: когда две хорды пересекаются внутри окружности, произведения отрезков каждой хорды равны между собой.

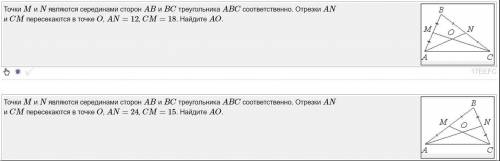
В данной задаче нам нужно найти длину отрезка АН, обозначенного на рисунке.

Давайте обозначим для удобства:
1) Отрезок АВ - h
2) Отрезок ВН - x
3) Отрезок АН - y

Исходя из свойства пересекающихся хорд, мы можем записать следующее равенство:

(х + 5) * (х - 1) = (h + 4) * (h - 2)

Нам нужно решить это уравнение относительно неизвестного значения х.

Произведение отрезков АВ и ВН дано выражение х + 5, так как х - это отрезок ВН, а на графике видно, что отрезок АВ больше этого значения.

Соответственно, произведение отрезков АН и ВН равно х - 1, так как х - 1 - это отрезок АН, а на графике видно, что отрезок ВН больше этого значения.

Аналогично, произведение отрезков АВ и АН равно (h + 4), так как (h + 4) - это отрезок АВ, а на графике видно, что отрезок АН больше этого значения.

Наконец, произведение отрезков ВН и АН равно (h - 2), так как (h - 2) - это отрезок ВН, а на графике видно, что отрезок АН больше этого значения.

Раскрывая скобки в уравнении, получим:

x^2 + 4x - 5 = h^2 + 2h - 8

После приведения подобных членов, уравнение примет вид:

x^2 + 4x - h^2 - 2h + 3 = 0

Обозначим это уравнение как (1).

По условию задачи, известно, что х > 1, а значит, нам нужно проверить, при каком диапазоне значений h и x уравнение (1) будет иметь решение.

Построим график квадратного уравнения y = x^2 + 4x - h^2 - 2h + 3.

Для этого запишем его в виде y = x^2 + 4x - (h^2 + 2h) + 3 и прировняем y к 0:

0 = x^2 + 4x - (h^2 + 2h) + 3

Теперь можем построить график этого уравнения, в котором ось ОХ будет отвечать за переменную x, а ось OY - за переменную y.

Построим график с помощью图ового редактора или калькулятора, чтобы проанализировать, при каких значениях h и x уравнение (1) имеет корни.

При анализе графика можно заключить, что уравнение (1) имеет решение при любых значениях h, при условии, что х > 1.

Таким образом, величина отрезка АН может принимать любые значения больше 2.

Ответ: Длина отрезка АН может быть любой, если она больше 2.