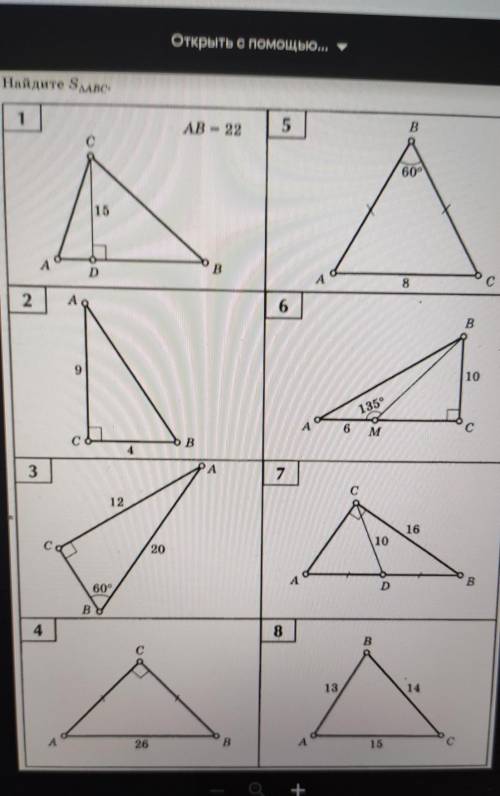
Геометрия, 9 класс. самостоятельная работа. решение треугольников нужно решение​

Добрый день!

Чтобы решить этот треугольник, нам понадобится использовать свойства треугольников и знания о сумме углов в треугольнике.

1. Вначале вспомним, что в треугольнике сумма всех его углов равна 180 градусов. Это свойство можно использовать для поиска неизвестных углов.

2. Как видно на изображении, у треугольника ABC имеются два известных угла: угол A = 30° и угол B = 90°. Остается найти третий угол треугольника.

3. Поскольку сумма углов треугольника равна 180°, мы можем найти третий угол, вычтя из 180° сумму уже известных углов:

Угол C = 180° - угол A - угол B
= 180° - 30° - 90°
= 60°

Таким образом, третий угол треугольника ABC равен 60°.

4. Перейдем к поиску сторон треугольника. Для этого применим теорему Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы (наибольшей стороны) равен сумме квадратов катетов (двух остальных сторон).

Исходя из изображения, катетом треугольника является сторона AB, а гипотенузой - сторона AC.

По условию, длина стороны AB равна 6 единицам.

Используя теорему Пифагора, мы можем записать соотношение:

AB² + BC² = AC²

Значение AB² у нас уже есть, это 6² = 36.

Заменяем значение AB² в уравнение:

36 + BC² = AC²

5. Теперь у нас есть только одно неизвестное - BC, и мы можем его найти. Для этого изымем из уравнения известный квадрат гипотенузы и возьмем корень от получившегося значения, чтобы найти сторону BC.

BC² = AC² - 36

BC² = 9² - 36

BC² = 81 - 36

BC² = 45

С помощью калькулятора или метода извлечения квадратного корня мы можем найти значение BC:

BC ≈ √45

BC ≈ 6.708

Таким образом, длина стороны BC приближенно равна 6.708 единицам.

6. Теперь мы знаем длины всех сторон треугольника ABC и можем сделать выводы о его свойствах.

- Сторона AB равна 6 единицам.
- Сторона BC равна приближенно 6.708 единицам.
- Сторона AC можно найти, используя теорему Пифагора:

AC² = AB² + BC²
AC² = 36 + 45
AC² = 81

Получается, что сторона AC равна 9 единицам.

Таким образом, мы определили все стороны треугольника ABC.