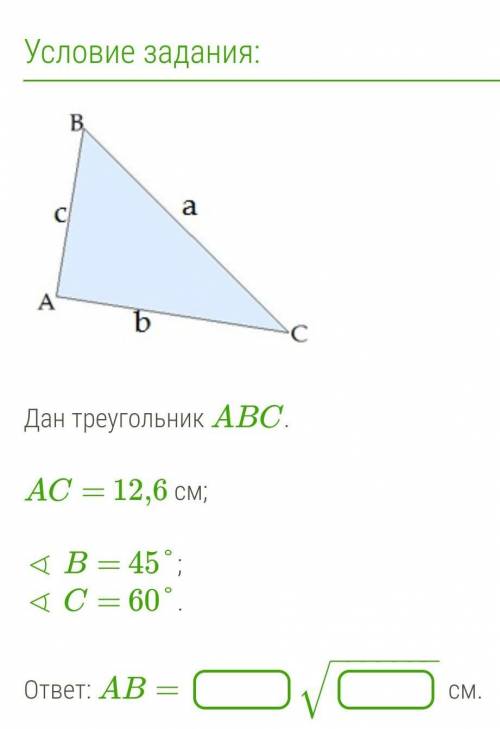
Геометрия 9 класс. Решите Дан треугольник ABC.
AC= 12,6 см;
∢ B= 45°;
∢ C= 60°.
ответ: AB=
−−−−−−−√ см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Нужна ли запятая перед «мышей» в предложении «Хитрая и самовлюблённая...
1 - ДАЮ 100 БОЛОВ Цель создания проекта: подготовка документа к печати(устанавливать...
2 - Скількома можна вибрати 1 рожеву або 1 червону троянду з 12 рожевих та...
3 - Определите, в выражении каких отношений участвуют предлоги в выделенных...
3 - Нужна ли запятая после «кошка» и после «мышей»в предложении «Хитрая и...
3 - Тезирек жасап бере аласындар ма? 1.Негизги акпаратты табу керек 2.Зат...
2 - испанский язык. Задние, поставить глаголы в нужную форму времени, либо...
1 - Всего лишь два примера! Найдите значение выражения...
3 - В каком ряду химических элементов усиливаются металлические свойства...
3 - Висловіть своє ставлення до дій західних держав у період югославської...
2
Известно, что угол ∠B равен 45° и угол ∠C равен 60°. В сумме углы треугольника равны 180°. Тогда ∠A равен:
∠A = 180° - ∠B - ∠C
∠A = 180° - 45° - 60°
∠A = 75°
Затем мы можем применить теорему синусов, чтобы найти сторону AB. Теорема синусов гласит:
a/sin(∠A) = b/sin(∠B) = c/sin(∠C)
Где a, b и c являются сторонами треугольника, а ∠A, ∠B и ∠C - соответствующими углами.
В нашем случае, мы ищем сторону AB, поэтому воспользуемся следующим соотношением:
AB/sin(∠A) = AC/sin(∠C)
Подставляем известные значения:
AB/sin(75°) = 12,6 см / sin(60°)
Теперь найдем sin(75°) и sin(60°). Значения синусов можно найти в специальной таблице, либо использовать калькулятор.
sin(75°) = 0,96593 (округляем до пятого знака после запятой)
sin(60°) = 0,86603 (округляем до пятого знака после запятой)
Подставляем найденные значения:
AB/0,96593 = 12,6 см / 0,86603
После дальнейших вычислений, получаем:
AB ≈ 12,6 см * 0,96593 / 0,86603
AB ≈ 14,04 см
Итак, длина стороны AB треугольника ABC составляет около 14,04 см. (округляем до двух знаков после запятой)