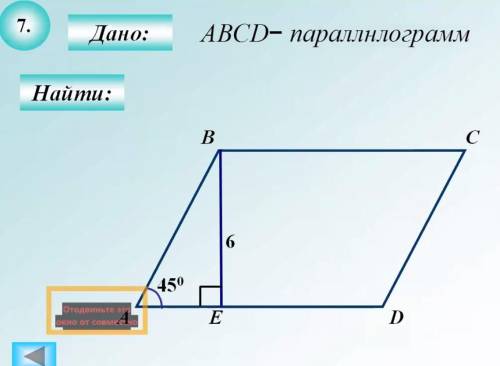
геометрия 8 класс, там где найти, там сторону CD надо,

Для того чтобы найти сторону CD, нам понадобится использовать свойство пропорциональности в треугольниках.

Для начала, обратимся к данному треугольнику DEF и рассмотрим две вертикальные прямые DE и BC. Воспользуемся одним из свойств подобных треугольников, которое гласит, что параллельные прямые, пересекающие стороны треугольников, порождают пропорциональные отрезки на этих сторонах. Это означает, что отношение длин отрезков DE и EF будет равно отношению длин BC и CD:

DE/EF = BC/CD

Теперь нам нужно найти известные значения и подставить их в эту формулу. По условию задачи, известны значения длин:

DE = 12 см
EF = 6 см
BC = 8 см

Подставим эти значения в формулу:

12/6 = 8/CD

Для удобства решения, можно упростить формулу путем сокращения общих делителей.

2 = 8/CD

Теперь нам нужно найти длину отрезка CD, для этого сделаем обратную операцию - разделим 8 на 2:

CD = 8/2 = 4 см

Таким образом, сторона CD равна 4 см.

Обратите внимание, что в данной задаче использовано свойство подобных треугольников, которое является основой геометрии и используется в решении многих задач.