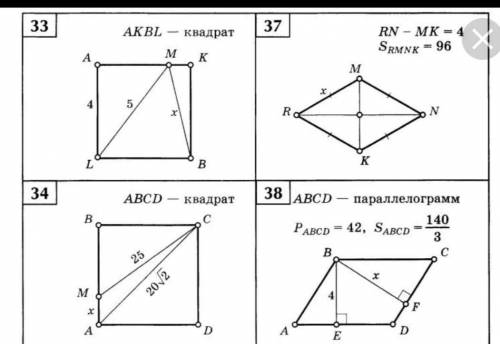
Геометрия 8 класс решить номера: 33,37,34

Конечно, я готов помочь вам с решением задач. Давайте посмотрим на каждый номер по отдельности.

33. Нам дан прямоугольник ABCD со сторонами AB = 6 см и BC = 8 см. Также известно, что точка M - середина стороны AB. Мы должны найти площадь треугольника MCD.

Для решения этой задачи, давайте воспользуемся тем фактом, что если точка M - середина стороны AB, то она делит сторону на две равные части. То есть, AM = MB = 3 см.

Теперь, чтобы найти площадь треугольника MCD, нам необходимо знать его высоту. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

Для нахождения высоты мы можем воспользоваться формулой площади треугольника: S = 0.5 * a * h, где S - площадь треугольника, a - длина основания, h - высота.

Мы знаем, что основание MC = 8 см. Теперь нам нужно найти высоту треугольника, которая будет являться перпендикуляром, опущенным из вершины D на сторону MC.

Давайте обратим внимание на прямоугольность треугольника MCD. Зная, что M - середина AB, мы можем сказать, что AM = 3 см, и MB = 3 см.

Также, так как треугольник прямоугольный, мы можем воспользоваться теоремой Пифагора: c^2 = a^2 + b^2, где c - гипотенуза, а и b - катеты.

В нашем случае, AD будет являться гипотенузой, а AM и MC - катетами. То есть, AD^2 = AM^2 + MC^2.

Подставляя известные значения, получим AD^2 = 3^2 + 8^2 = 9 + 64 = 73.

Теперь, чтобы найти высоту треугольника, нам необходимо найти AD. Используя теорему Пифагора, можем найти AD = √73, что примерно равно 8.54 см.

Теперь у нас есть основание MC = 8 см и высота AD ≈ 8.54 см. Подставляя эти значения в формулу площади треугольника, получим S = 0.5 * 8 * 8.54 = 34.16.

Ответ: Площадь треугольника MCD ≈ 34.16 квадратных сантиметра.

37. Нам нужно найти площадь кольца внешнего и внутреннего радиусов r1 и r2 соответственно. Для этого мы можем воспользоваться формулой площади кольца: S = π * (r1^2 - r2^2), где π ≈ 3.14.

В нашем случае, внешний радиус r1 = 10 см, а внутренний радиус r2 = 6 см. Подставляя значения в формулу, получим:

S = 3.14 * (10^2 - 6^2) = 3.14 * (100 - 36) = 3.14 * 64 = 200.96

Ответ: Площадь кольца равна 200.96 квадратных сантиметра.

34. Нам дан прямоугольник ABCD, в котором сторона AB равна 12 см, а сторона BC равна 8 см. Требуется найти площадь прямоугольника, описанного вокруг треугольника ACD.

Чтобы найти площадь прямоугольника, описанного вокруг треугольника, нам нужно знать его размеры.

Для этого воспользуемся тем фактом, что прямоугольник, описанный вокруг треугольника, имеет противоположные стороны, которые проходят через середины сторон треугольника.

В нашем случае, сторона AB является диагональю прямоугольника, описанного вокруг треугольника ACD.

Используя теорему Пифагора, можем найти длину диагонали AB: AB^2 = AC^2 + BC^2.

Подставляя известные значения, получим AB^2 = 12^2 + 8^2 = 144 + 64 = 208.

Теперь найдем AB: AB = √208, что примерно равно 14.42 см.

Также, мы знаем, что противоположные стороны прямоугольника, описанного вокруг треугольника, равны соответствующим сторонам треугольника.

То есть, сторона AD = 12 см и сторона CD = 8 см.

Теперь у нас есть сторона AB ≈ 14.42 см, сторона AD = 12 см и сторона CD = 8 см.

Подставляя эти значения в формулу площади прямоугольника, получим S = AB * AD = 14.42 * 12 = 173.04.

Ответ: Площадь прямоугольника, описанного вокруг треугольника ACD, равна 173.04 квадратных сантиметра.