Геометрия 8 класс. мне кажется ни кто не решит​

6

Объяснение:

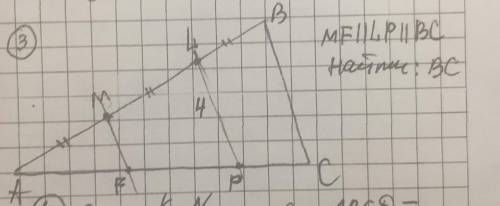
Прямые LP и BC параллельны => углы mlp и lbc равны.

Треугольники alp и abc подобны по 2 углам ( общий угол maf и попарно равные углы mlp и lbc)

Коэффициент подобия треугольников будет равен 3x / 2x (отношение сторон против угла C) = 3/2 => отношение bc /  lp (против угла A) = 3/2

BC/4 = 3/2 ; BC = 6

6

Объяснение:

ΔALP ≈ΔABC :  ∠А-бщий,  ∠ALP=∠ABC при LP ║BC , Ав-секущая.

BC=6