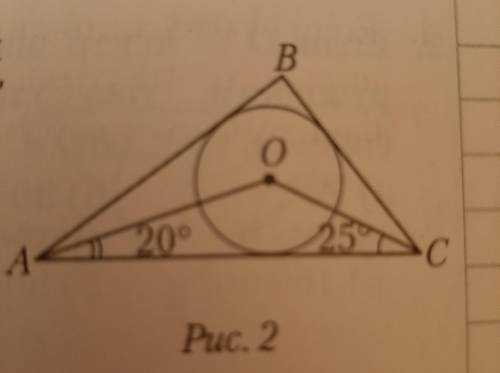
Если О - центр вписанной окружности треугольника ABC, то угол ABC равен...
Другие вопросы по теме Геометрия
Популярные вопросы
- Позначити частини мови.Друзі вийшли на велику галявину....
3 - ЛІся от глав-грамматическая связь вы-JMUщью окончания, а также...
1 - X² + y² +8=4(y - x).4x² + y² +2=2(2x-y)....
2 - Приведите примеры восстановления воинскими формированиями необходимых...
3 - Запишите предложения, укажите личные местоимения, которые отвечают...
2 - Составьте химическое уравнение реакции...
2 - Sin(arccos(-4/5))= Обсислити...
1 - с сочинением на тему «Что значит быть сплоченным?» Приведите 2...
1 - Полоний испытывае т ɑ-распад. Запишите реакцию этого радиоактивного...
1 - за ответ Задача: один насос працюючи може відкачати 1512л води...
2
2. По свойствам биссектрисы следует, что она делит углы треугольника пополам, то есть AH делит угол BAC на равные углы BAH = HAC = 20°, а биссектриса CE делит угол BCA на равные углы BCE = ECA = 25°;
3. Рассмотрим треугольник AOC: сумма углов треугольника 180°, тогда угол О = 180° - (HAC + ECA) = 180-45=135°;
4. Найдём больший угол АОС, который равняется 360°-меньший угол АОС = 360-135 = 235°;
5. Рассмотрим четырёхугольник АОС. Сумма углов четырехугольника равна 360°, угол BAH = 20°, угол ECB = 25°, тогда угол ABC = 360°-(ECB+BAH+AOC) = 360°-(45°+235°)= 80°;
ответ: угол ABC = 80°.
Объяснение:
АО и СО биссектрисы. угол А=20*2=40, угол С 25*2=50, угол В=180-(40+50)=90.
угол АВС=90°.