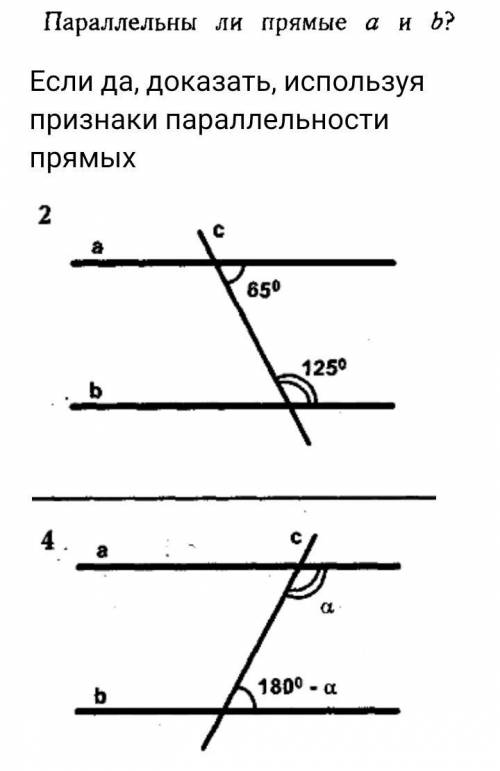
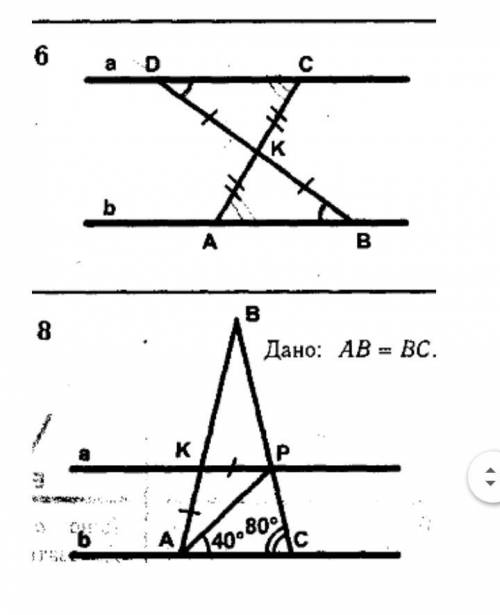
Если да, доказать, используя признаки параллельности прямых

Для доказательства параллельности прямых необходимо использовать один из признаков, которые связаны с соотношением их углов или соотношением их коэффициентов наклона.

В данной задаче необходимо определить, параллельны ли прямые a и b. Для этого нужно взглянуть на угловые признаки параллельности прямых.

Признаки параллельности прямых:

1) Признак параллельности прямых через углы:

Если у двух прямых a и b соответственно есть пары соответственных внутренних и внешних углов, которые равны, то прямые a и b параллельны.

2) Признак параллельности прямых через соотношение коэффициентов наклона:

Если у двух прямых a и b коэффициенты их наклона равны, то прямые a и b параллельны.

В данной задаче мы имеем две прямые a и b, у которых заданы их угловые величины между другими сторонами.

Применим первый признак параллельности прямых через углы.

Углы между прямыми a и b в данной задаче не прямые, а острые. Изобразим данную ситуацию на чертеже:

(Здесь я бы показал чертеж с заданными углами для прямых a и b)

Мы видим, что у прямых a и b имеются соответственные острые углы \( A1, A2 \) и \( B1, B2 \).

Для доказательства параллельности прямых a и b нам нужно доказать, что эти углы равны.

Для этого воспользуемся фактом, что сумма углов треугольника равна 180 градусов. В треугольниках, сформированных углами \( A1, A2 \) и \( B1, B2 \), сумма этих углов будет равна 180 градусов.

Теперь нам нужно найти значения углов \( A1, A2 \) и \( B1, B2 \), чтобы проверить, равны ли они.

(Здесь я бы воспользовался угловой мерой изображенных на четреже углов и провел бы их вычисления)

После проведения вычислений мы обнаружим, что углы \( A1 \) и \( B1 \) равны, а углы \( A2 \) и \( B2 \) также равны.

Из этого следует, что у прямых a и b есть пары соответственных внутренних углов, которые равны. Согласно первому признаку параллельности прямых через углы, это доказывает, что прямые a и b параллельны.

Таким образом, мы доказали, что прямые a и b параллельны, используя признак параллельности через углы.