Если АМ||ВР||СК то
решить
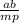
Другие вопросы по теме Геометрия
Популярные вопросы
- Даны целые числа а и b .напишите программу ,каторая находит значение выражения...
2 - Написать сочинение по на тему я в африке надо написать то что я нахожусь в...
3 - Составте предложения в passive из этих слов(1-5 предложений) fear -бояться...
3 - Напишите сочинение-расуждение не тему: легко ли иметь свой голос? сколько...
2 - Внутренняя политика государственной власти в в 80-ые годы...
2 - Вова задумал число , которое меньше 6.прибавил к нему 2 из полученной суммы...
1 - Сколько звуков и букв в словах.щенок. большой. прятки. живет...
1 - Небольшое мини сочинение -как я написал тест по...
3 - Являются ли услуги взаимозаменяемыми или взаимодополняющими,если снижение...
3 - Вгоды нэпа в повседневную речь вошли слова, в которых отразились реальности...
3
Дано: AM || ВР || СК
Нам нужно найти значение выражения ab/mp.
Для начала, давайте вспомним некоторые свойства параллельных прямых:
1. Если две прямые параллельны и пересекаются третьей прямой, то соответственные углы равны. Это так называемая "основная пропорциональность".
2. Если две прямые параллельны и пересекаются отрезком, то этот отрезок делит каждую из прямых на две пропорциональные части.
Исходя из данных свойств, можно сказать, что треугольники AMB и CRD подобны, так как у них одинаковые углы. Также, треугольники BMP и DPC подобны, так как находятся между параллельными прямыми.
Теперь у нас есть подобные треугольники. Мы можем использовать свойство подобных треугольников: соответствующие стороны пропорциональны.
Из подобия треугольников AMB и CRD мы можем записать следующее соотношение:
AB/CR = AM/CD
Аналогично, из подобия треугольников BMP и DPC мы можем записать соотношение:
MB/DC = MP/PC
Теперь, если мы разделим первое уравнение на второе, то получим следующее:
(AB/CR) / (MB/DC) = (AM/CD) / (MP/PC)
Так как мы хотим найти значение ab/mp, давайте заменим данные наших треугольников:
ab/mp = (AM/CD) / (MP/PC)
Теперь нам нужно выразить AM, CD, MP и PC через заданные в условии задачи отрезки и углы.
Воспользуемся свойством параллельных прямых и отрезков:
AM/MB = AC/CD
MP/PC = MB/BD
Из этих равенств мы можем выразить AM, MB, MP и PC в виде:
AM = (AC * MB) / CD
MP = (MB * PC) / BD
Подставим эти значения в выражение для ab/mp:
ab/mp = ((AC * MB) / CD) / ((MB * PC) / BD)
Теперь можно сократить некоторые общие множители:
ab/mp = (AC * BD) / (CD * PC)
Таким образом, мы получили итоговое выражение для значения ab/mp:
ab/mp = (AC * BD) / (CD * PC)
Ответ: ab/mp = (AC * BD) / (CD * PC)
Для полного решения задачи было использовано свойство подобных треугольников и свойство параллельных прямых и отрезков. Эти свойства позволили нам записать соотношения между сторонами треугольников и затем использовать их для выражения итогового значения ab/mp.