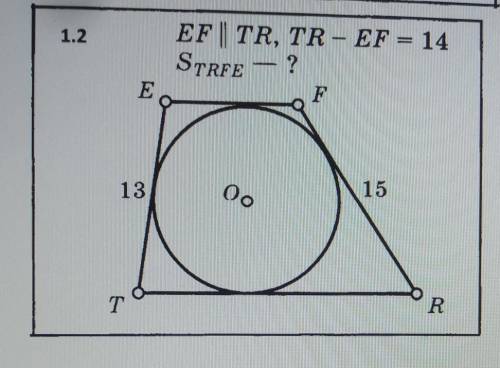
EF||TR, TR - EF = 14
S∆TRFE - ?
FR =15
ΕT = 13

Давайте разберем каждую часть вопроса по порядку:

1. EF||TR: Это значит, что отрезки EF и TR параллельны. Параллельные прямые имеют одинаковый наклон, поэтому углы, которые они образуют с другими прямыми, будут одинаковыми.

2. TR - EF = 14: Здесь дано, что разность отрезков TR и EF равна 14. Это значит, что если мы вычтем длину EF из длины TR, мы получим 14.

3. FR = 15: Здесь дано, что отрезок FR равен 15.

4. ΕT = 13: Здесь дано, что отрезок ΕT равен 13.

Теперь, если мы хотим найти значение выражения S∆TRFE, то нам нужно знать, что это значит. S∆TRFE представляет собой площадь треугольника TRFE.

Чтобы найти площадь треугольника, нам нужно знать его основание и высоту. Основание треугольника TRFE - это отрезок TR. А высоту мы можем найти, заметив, что EF параллельна TR и перпендикулярна FT.

Теперь перейдем к решению:

1. Заметим, что в треугольнике TRF угол FTR равен 90 градусов, так как EF перпендикулярна FT (обычно перпендикулярные прямые образуют прямой угол).
2. В треугольнике TRF у нас есть две известные стороны: TR = 14 + EF и FR = 15. Мы можем использовать теорему Пифагора, чтобы найти третью сторону TF.
TF² = FR² + TR²
TF² = 15² + (14 + EF)²
TF² = 225 + (196 + 28EF + EF²)
TF² = 421 + 28EF + EF²

3. В треугольнике TEF у нас есть две известные стороны: ΕT = 13 и EF. Мы можем использовать теорему Пифагора, чтобы найти третью сторону TF.
TE² = ΕT² + EF²
13² = 169 = EF² + EF²
2EF² = 169
EF² = 84.5
EF ≈ 9.20

4. Теперь мы знаем, что TF² = 421 + 28EF + EF² и можем подставить значение EF:
TF² = 421 + 28(9.20) + 84.5
TF² = 421 + 257.6 + 84.5
TF² ≈ 763.1
TF ≈ 27.65

5. Чтобы найти площадь треугольника TRFE (S∆TRFE), мы можем использовать формулу для площади треугольника: S = 0.5 * основание * высота.
Основание треугольника TRFE: TR = 14 + EF ≈ 14 + 9.20 ≈ 23.20
Высота треугольника TRFE: FT = TF ≈ 27.65
S∆TRFE ≈ 0.5 * 23.20 * 27.65 ≈ 319.86

Таким образом, ответом на вопрос "S∆TRFE - ?" будет около 319.86 (значение может быть округлено).