Двугранный угол при боковом ребре правильной четырехугольной пирамиды 120°. Нати угол между ребром и основанием

Двугранный угол при боковом ребре правильной четырехугольной пирамиды 120°. Найти угол между ребром и основанием

Объяснение:

1) Пусть ВР⊥МС. Соединим Р и D.

ΔВРС=ΔDРС по 2 сторонам и углу между ними :РС-общая, ВС=DC как стороны квадрата ,∠РСВ=∠РСD  как углы равных треугольников боковых граней.. Поэтому DР⊥МС и ∠DРВ- линейный угол двугранного угла при боковом ребре,∠DРВ=120°.

2) Углом  между ребром  МС и основанием АВСD будет угол между наклонной МС и ее проекцией СО⇒ ∠РСО.

РО∈(ВРD) ⇒РО⊥МС  , значит ΔОРС-прямоугольный  , sin(∠РСО)= .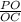

3) Пусть РВ=РD=х , для ΔBDP  применим т. косинусов

BD²=х²+х²-2х²cos120  ( cos120=0,5)  , BD²=3x²   , BD=x√3.

Значит , половина диагонали квадрата ,   ОС=  .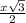

4) РО для ΔBDP  является медианой, высотой биссектрисой. Поэтому    ΔОРВ- прямоугольный, ∠ОРВ=60° →∠ОВР=30°⇒ катет РО= .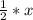

5)  sin(∠РСО)=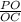  ,   sin(∠РСО)= 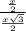= 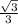 ,  ∠РСО=arcsin .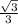