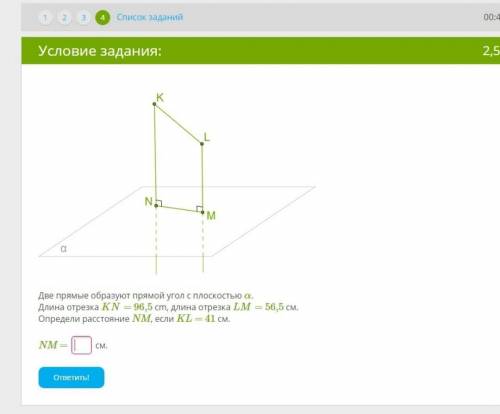
Две прямые образуют прямой угол с плоскостью α.
Длина отрезка KN= 96,5 cm, длина отрезка LM= 56,5 см.
Определи расстояние NM, если KL = 41 см.

Чтобы решить эту задачу, нужно использовать основное свойство прямого угла и плоскости. По условию, у нас есть две прямые, которые образуют прямой угол с плоскостью α. То есть, угол KNL равен 90 градусов. У нас также даны длины отрезков KN, LM и KL. Мы хотим найти длину отрезка NM. Для начала, давайте рассмотрим треугольник KNM. Мы знаем длины отрезков KN и LM, и хотим найти длину отрезка NM. Одно из основных свойств прямого угла гласит, что его биссектриса является перпендикуляром к обоим сторонам угла. Поэтому отрезок KL является биссектрисой угла KNL. Так как длина отрезка KL равна 41 см, то отрезок KN и отрезок NL также равны 41 см. Теперь мы можем применить теорему Пифагора для треугольника KNM, чтобы найти длину отрезка NM. Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае, гипотенуза - это отрезок KM, катеты - отрезки KN и NM. Используем теорему Пифагора: KN^2 + NM^2 = KM^2 Подставляем известные значения: (41^2) + (NM^2) = (96.5^2) Решаем уравнение, чтобы найти NM: 1681 + NM^2 = 9322.25 NM^2 = 9322.25 - 1681 NM^2 = 7641.25 NM = √7641.25 NM ≈ 87.47 см Таким образом, длина отрезка NM примерно равна 87.47 см.