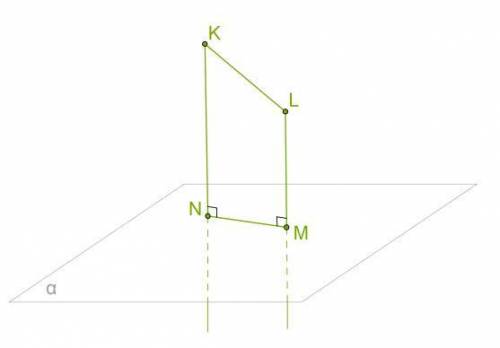
Две прямые образуют прямой угол с плоскостью α. Длина отрезка KN= 34,5 cm, длина отрезка LM= 26,5 см.
Рассчитай длину NM, если KL = 10 см
Другие вопросы по теме Геометрия
Популярные вопросы
- ответ напишите. 1.абай атамыз қандай болған? 2.абай ата не туралы...
2 - Продолжите предложение.. переходит от аграрного(традиционного)общества...
3 - Формирование климата в различных регионах земного шара происходит...
2 - Exercise 6. задайте вопросы к выделенным словам в ответах: 1. the...
3 - Как сделать яз номер 18 can you describe these animls there are...
2 - exercise 5. вставьте предлоги или наречия: 1. every tooth consists…a...
1 - 2) y = -x2 + 2x + 3; побудуйте графік функції...
1 - Решить дифференциальное уравнение...
2 - Объясните, что такое энтальпия, энтропия, энергия гиббса простыми...
3 - Подчеркнуть подлежащие и сказуемое в предложении добра гнушаться-с...
2
1. Поскольку две прямые образуют прямой угол с плоскостью α, угол LKN является прямым углом. Это означает, что угол NKL также является прямым углом и сумма всех углов в треугольнике NKL равна 180 градусов.
2. Известно, что KL = 10 см, KN = 34,5 см и LM = 26,5 см. Используем эти данные для нахождения длины NM.
3. Обратимся к треугольнику NKL. У нас есть один прямой угол и две стороны (KN и KL), поэтому мы можем использовать теорему Пифагора, чтобы найти длину стороны NL.
По теореме Пифагора:
KN^2 = KL^2 + NL^2
34,5^2 = 10^2 + NL^2
1190,25 = 100 + NL^2
NL^2 = 1190,25 - 100
NL^2 = 1090,25
Теперь найдем квадратный корень из NL^2, чтобы получить длину NL:
NL = √1090,25
NL ≈ 33 см (округляем до ближайшего сантиметра).
4. Таким образом, длина отрезка NM равна сумме длин отрезков NL и LM:
NM = NL + LM
NM ≈ 33 см + 26,5 см
NM ≈ 59,5 см
Ответ: Длина NM составляет примерно 59,5 см.