Две окружности радиусов 12 и 20 внешне касаются в точке к. обе окружности касаются одной прямой в точках а и с и касаются другой прямой

Question

Геометрия: Две окружности радиусов 12 и 20 внешне касаются в точке к. обе окружности касаются одной прямой в точках а и с и касаются другой прямой в точках в и d . точки а и в лежат на первой окружности, точки с и d- на второй. найти расстояние между прямыми ав и сd.

alenkakempelma7keaa · Answer

Продолжим касательные до их пересечения в т.Р.

ОА⊥АС и О1С⊥АС ( радиусы, проведенные в точку касания.

Из т.О проведем параллельно АС прямую до пересечения с СО1 в т.Н.

Четырехугольник АОНС - прямоугольник. СН=АО=r=12 ⇒

О1Н=20-12=8

⊿ ОНО1 - прямоугольный. ОО1=12+20=32.

По т.Пифагора

ОН=√(OO1²-O1H²)=√(32²-8²)=√960=8√15

cos∠HOO1=OH:OO1=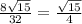 $\frac{8 \sqrt{15} }{32} = \frac{ \sqrt{15} }{4}$

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.⇒

РС=РD, PA=PB ⇒ BD=AC=8√15

∆ СРD равнобедренный, ∆ РАВ равнобедренный ⇒

биссектриса АО1 перпендикулярна АВ и СD

∠СРО1=∠DPO1

Расстояние между АВ и СD - длина общего между ними перпендикуляра.

Проведем ВМ || РО1

ВМ⊥АВ и ВМ⊥СD.

∆ ВМD прямоугольный. ∠МВD=∠O1PD

ВМ=BD•cosO1PD=8√15•√15:4=30