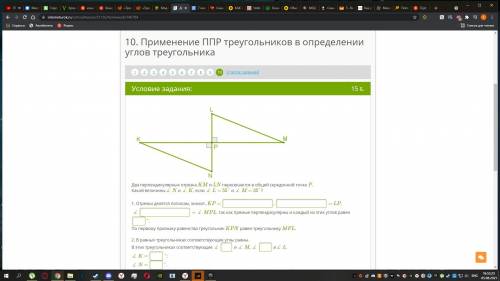
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P. Какой величины∡ N и ∡ K, если ∡ L = 55° и ∡ M = 35°?

1. Отрезки делятся пополам, значит, KP =
,
= LP,
∡
= ∡ MPL, так как прямые перпендикулярны и каждый из этих углов равен
°.
По первому признаку равенства треугольник KPN равен треугольнику MPL.

2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡
и ∡ M, ∡
и∡ L.
∡ K =
°;
∡ N =
°.

Keyanplay1    3   05.08.2021 17:20    14